What is the sum of an infinite resistor ladder with geometric progression?

Question

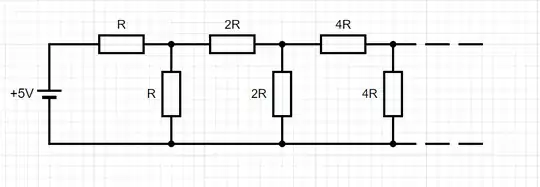
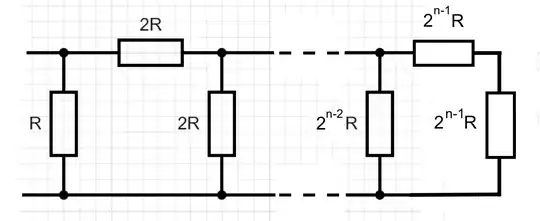
I am trying to solve for the equivalent resistance $R_{\infty}$ of an infinite resistor ladder network with geometric progression as in the image below, with the size of the resistors in each section double the size of the previous section.

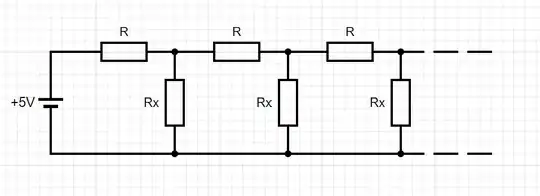
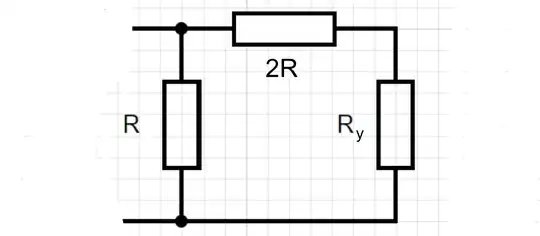
For those not familiar with the calculations for summing resistors, here is a quick recap: there are standard solutions in the literature for infinite resistor ladder networks without geometric progression such as the one below (where $R_x$ is simply $R$ multiplied by a factor of $x$).

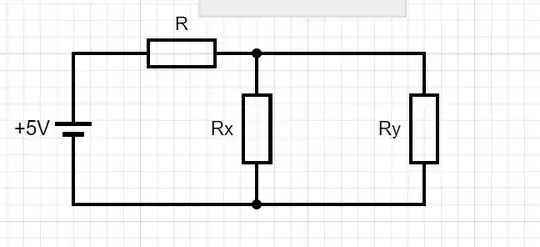
The trick here is to replace all of the resistors to the right of the first two with a single resistor of value $R_y$ ...

... and realise that because the network is infinite, the first two resistors make no difference and so $R_{\infty} = R_y$. The problem becomes finding the combined resistance of the two resistors in parallel $R_x$ and $R_y$ which by the rules of adding resistors is $\frac{R_y R_x}{R_y +R_x}$ and simply adding them to the resistor $R$ that is in series with the rest. We then get the equation:

$$R_{\infty} = \frac{R_y R_x}{R_y +R_x} + R \rightarrow \frac{R_{\infty} R_x}{R_{\infty} +R_x} + R$$ and solve for $R_{\infty}$ using the quadratic solution. The result is:

$$R_{\infty}= \frac R 2 (1+\sqrt{4x +1}).$$

For $R=1$ and $x=1$, the result is $(1+\sqrt{5})/2$ which interestingly enough is the golden ratio.

For the original problem with the geometric progression, all the rungs are not the same and we can not use the standard trick. Doing it the hard way the first few steps of a small finite geometric ladder are:

First rung $= 2$,
First 2 rungs $= 9/5 = 1.8$,
First 3 rungs $= 41/23 \approx 1.78260$,
First 4 rungs $= 187/105 \approx 1.78095$,
First 5 rungs $= 853/479 \approx 1.78079$,

which appears to be converging rapidly toward somewhere around $1.7$. It is known by the properties of resistors that the result must be between $1<R_{\infty} <2$.

After investigating the pattern for a while, it emerges that there is a recursive relationship. If we represent the irreducible fraction for the resistance of each step as $A'/B'$ and the previous step as $A/B$, then the recursive relationship is $$\frac {A'}{B'} = \frac {4A+B}{2A+B}.$$

For example, the first step has a resistance of $2/1$. The next step has a total resistance of $\frac{4 \cdot 2 +1}{2 \cdot 2 +1} = \frac 9 5$. The result always appears to be an irreducible fraction without requiring a reduction step. This is where I get stuck. It does not seem to be possible to find the limit as $n$ goes to infinity for a recursive formula, so I was wondering how to convert the recursive formula to a closed form?

P.S. Should I remove the preamble where I recap the formulas for finding the equivalent resistance of resistor circuits? I added it because I assumed the mathematic experts here are not necessarily physics experts.

P.P.S. Just for fun I wrote this short Python code to carry out the iteration of the recursive function and compare the result to the theoretical limit (given in the answers) of $(3+\sqrt{17})/4$:

import math
def iterate_formula(n):
    A, B = 2, 1
    for _ in range(n):
        A_prime = 4A + B
        B_prime = 2A + B
        A, B = A_prime, B_prime
        print(f"After iteration {_+1}, A' = {A}, B' = {B}, and A'/B' = {A/B:.80f}")
Call the function with the number of iterations you want
iterate_formula(16)
x=(3+math.sqrt(17))/4
print("Compare:")
print(f"Infinite Sum = {x:.80f}")

After just 15 iterations, Python (without special import modules) can not distinguish between the iterated result and the limit at infinity.

Answer 1

You can use the same trick as you did for the fixed factor case by observing that the resistance of the circuit

$\hspace{10em}\text{Figure 1.}$

is exactly twice the resistance of the circuit

$\hspace{10em}\text{Figure 2.}$

which I'll take to be $\ T_\infty\,\big(=R_\infty-R\,\big)\ .$ So when you now replace all the resistors to the right of the first two with a single one with resistance $\ R_y\ $

you'll have $\ R_y=2T_\infty\ $, from which you get $$ T_\infty=\frac{2R\big(R+T_\infty\big)}{3R+2T_\infty}\ ,\\ $$ or, ultimately, $$ T_\infty=\left(\frac{\sqrt{17}-1}{4}\right)R\ $$ and $$ R_\infty=\left(\frac{3+\sqrt{17}}{4}\right)R\ $$

Alternatively, you can also find a solution to your recursion $$ \frac{ A_{n+1}}{B_{n+1}}=\frac{4A_n+B_n}{2A_n+B_n} $$ with $\ A_1=9, B_1=5\ $ by replacing it with a pair of recursions, \begin{align} A_{n+1}&=4A_n+B_n\tag{1}\label{e1}\\ B_{n+1}&=2A_n+B_n\tag{2}\label{e2}\ . \end{align} Substituting for $\ B_n=2A_{n-1}+B_{n-1}\ $ from equation (\ref{e2}) into equation (\ref{e1}) gives $$ A_{n+1}=4A_n+2A_{n-1}+B_{n-1}\tag{3}\label{e3}\ , $$ and substituting $\ B_{n-1}=A_n-4A_{n-1}\ $ from equation (\ref{e1}) into equation (\ref{e3}) gives $$ A_{n+1}=5A_n-2A_{n-1}\ , $$ a second-order linear recursion in $\ A_n\ $ with initial conditions $\ A_0=2,A_1=9\ .$ This has solution $$ A_n={\small\left(1+\frac{4}{\sqrt{17}}\right)\left(\frac{5+\sqrt{17}}{2}\right)^n+\left(1-\frac{4}{\sqrt{17}}\right)\left(\frac{5-\sqrt{17}}{2}\right)^n}\ , $$ from which we get \begin{align} \lim_{n\rightarrow\infty}\frac{A_n}{B_n}&=\lim_{n\rightarrow\infty}\frac{A_n}{A_{n+1}-4A_n}\\ &=\lim_{n\rightarrow\infty}\frac{1}{\frac{A_{n+1}}{A_n}-4}\\ &=\frac{1}{\frac{5+\sqrt{17}}{2}-4}\\ &=\frac{3+\sqrt{17}}{4}\ , \end{align} which gives the same value for $\ R_\infty\ $ as above.

Homogeneity of $\ T_\infty\ $ in $\ R\ $

As pointed out by An_Elephant in a comment below (and similarly mentioned by Gonçalo in his answer), it's not completely obvious that the resistance of the circuit depicted in Figure $1$ is exactly twice that of the circuit depicted in Figure $2$. Here's a proof by induction that the resistance of a finite version of this ladder with $\ n\ $ rungs is indeed homogeneous of degree $1$ in the variable $\ R\ .$ Taking the limit as $\ n\rightarrow\infty\ $ (assuming it exists$\left.\right.^\color{red}{\dagger}$) then shows that the resistance of the infinite ladder depicted in Figure $2$ is likewise homogeneous of degree $1$ in $\ R\ .$

Let $\ f_n(R)\ $ be the resistance of the following $ n$-rung ladder

in which the $\ (n-1)$-rung ladder to the right of the first two resistors will have resistance $\ f_{n-1}(2R)\ .$ Thus, \begin{align} f_n(R)&=\frac{1}{\frac{1}{R}+\frac{1}{2R+f_{n-1}(2R)}}\\ &=\frac{2R^2+Rf_{n-1}(2R)}{3R+f_{n-1}(2R)}\ \text{ and}\\ f_1(R)&=R\ . \end{align} Therefore, $\ f_1(\lambda R)=\lambda R=\lambda f_1(R)\ $ for all $\ \lambda,R\ ,$ and if $\ f_{n-1}(\lambda R)=\lambda f_{n-1}(R)\ $ for all $\ \lambda,R\ ,$ then \begin{align} f_n(\lambda R)&=\frac{2(\lambda R)^2+\lambda Rf_{n-1}(2\lambda R)}{3\lambda R+f_{n-1}(2\lambda R)}\\ &=\lambda\left(\frac{2R^2+Rf_{n-1}(2R)}{3R+f_{n-1}(2R)}\right)\\ &=\lambda f_n(R)\ . \end{align} It follows by induction that $\ f_n(\lambda R)=\lambda f_n(R)\ $ for all $\ \lambda,R\ $ and all $\ n\ ,$ and therefore that $\ T_\infty=\lim_\limits{n\rightarrow\infty}f_n(R)\ $ is homogeneous of degree $1$ in $\ R\ .$

$\left.\right.^\color{red}{\dagger}$ Which it must do for the resistance of the infinite version of the ladder to be properly defined.

Answer 2

This is not a rigorous answer.

Let $R_{\infty}(R)$ denote the equivalent resistance of the first resistor ladder network; then, using the same method you used for calculating the equivalent resistance of the second network, we obtain the following relation: $$ R_{\infty}(R)=R+\frac{RR_{\infty}(2R)}{R+R_{\infty}(2R)}, \tag{1} $$ where $R_{\infty}(2R)$ is the equivalent resistance of the first network when $R$ is replaced with $2R$. Now comes the step that must be justified: if we assume that $R_{\infty}(2R)=2R_{\infty}(R)$, then we can solve Eq. $(1)$. The result is $$ R_{\infty}(R)=\left(\frac{3+\sqrt{17}}{4}\right)R\approx 1.78078 R, \tag{2} $$ which is very close to the result you found for the finite ladder with $5$ rungs.

Answer 3

For brevity, let $P(r_1, r_2) = \frac{r_1r_2}{r_1 + r_2}$ denote the combined resistance of two resistors in parallel.

Let $f(n)$ denote the resistance of a finite resistor ladder with $n$ rungs. Then:

$$f(1) = R + R = 2R$$ $$f(2) = R + P(R, 2R + 2R) = \frac{9}{5}R$$ $$f(3) = R + P(R, 2R + P(2R, 4R + 4R)) = \frac{41}{23}R$$ $$f(4) = R + P(R, 2R + P(2R, 4R + P(4R, 8R + 8R))) = \frac{187}{105}R$$ $$f(5) = R + P(R, 2R + P(2R, 4R + P(4R, P(8R, 16R + 16R)))) = \frac{853}{479}R$$

As you have already found.

Let $x_n$ denote the number such that $f(n) = R + P(R, x_nR)$. Then plugging in the definition of $P$ and solving for $x_n$ gives:

$$x_n = \frac{f(n) - R}{2R - f(n)} = \frac{\frac{f(n)}{R} - 1}{2 - \frac{f(n)}{R}}$$

This gives us:

$$x_1 = \infty$$ $$x_2 = 4 = 2\frac{f(1)}{R}$$ $$x_3 = \frac{18}{5} = 2\frac{f(2)}{R}$$ $$x_4 = \frac{82}{23} = 2\frac{f(3)}{R}$$ $$x_5 = \frac{374}{105} = 2\frac{f(4)}{R}$$

There's an obvious pattern here: $x_n = 2\frac{f(n-1)}{R}$. I'll just be lazy and assume it without rigorous proof. Plugging in the expression for $x_n$ gives us:

$$\frac{f(n) - R}{2R - f(n)} = 2\frac{f(n-1)}{R}$$

And solving for $f(n)$ in terms of $f(n-1)$ gives:

$$\frac{f(n)}{R} = \frac{4\frac{f(n-1)}{R} + 1}{2\frac{f(n-1)}{R} + 1}$$

This is a recursive formula similar to the one you found, but without separate $A$ and $B$ sequences.

Now, let $L = \lim_{n \to \infty} \frac{f(n)}{R}$ (assuming that the limit exists). For sufficiently large $n$, both $f(n-1)$ and $f(n)$ approach $L$, so:

$$L = \frac{4L + 1}{2L + 1}$$ $$L(2L + 1) = 4L + 1$$ $$2L^2 - 3L - 1 = 0$$

Applying the quadratic formula gives:

$$L = \frac{-(-3) \pm \sqrt{(-3)^2 - 4(2)(-1)}}{2(2)} = \frac{3 \pm \sqrt{17}}{4}$$

Choosing the - solution produces a negative number, which makes no physical sense, so we'll use the + solution. This gives us:

$$\boxed{\lim_{n\to\infty} f(n) = \frac{3 + \sqrt{17}}{4} R \approx 1.780776 R}$$