Simple bisection geometry

Question

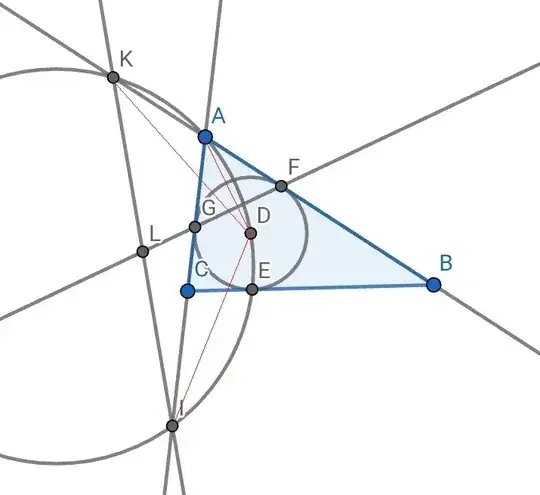
Let $\triangle ABC$ have incenter $D$ and let the incircle intersect sides $BC,AB,AC$ at $E,F,G$ respectively. Extend $AB$ and $AC$ to meet the circumcircle of $\triangle ADE$ at $K$ and $I$ respectively. Prove that $FG$ bisects $KI$.

I have solved this with barycentric coordinates, but I would like to see a synthetic solution as it may be more elegant.

We employ a barycentric coordinate syst¹em. We list the coordinates of the points that we know. Here $s$ denotes the semiperimeter of $\triangle{ABC}$, so $s=\frac{a+b+c}{2}$. \begin{align*} E = (0 : s-c : s-b) \\ F = (s-c : 0 : s-a) \\ G = (s-b : s-a : 0) \\ D = (a : b : c) \\ A = (1 : 0 : 0) \\ B = (0 : 1 : 0) \\ C = (0 : 0 : 1). \end{align*} We also know that the equation of $AB$ is $z=0$ and the equation of $AC$ is $y=0$. Thus we simply have to find the equation of the circumcircle of $\triangle{ADE}$ and the equation of line $KI$ and $FG$ and show that it intersects at the desired points.

1/ You might want to set up the question properly first. 2/ You might want to state your barycentric coordinates solution. — Calvin Lin, Nov 27 '23 at 18:38
smells like Menelaus to me - although one could argue it follows from coordinate bashing. — dezdichado, Nov 27 '23 at 20:21

score 2 · Answer 1 · answered Nov 28 '23 at 08:33

Note that $$\angle DIK = \angle DAF = \frac 12 \angle CAB = \angle CAD = \angle IKD,$$ hence $DK=DI$. Therefore the projection of $D$ onto $IK$ is the midpoint of $IK$. Note that $F$ is the projection of $D$ onto $AK$ and $G$ is the projection of $D$ onto $AI$. By Simson theorem, these three projections are collinear (they lie on the Simson line of $D$ with respect to $\triangle AKI$). This shows that $GF$ passes through the midpoint of $IK$.

score 1 · Answer 2 · answered Nov 28 '23 at 06:43

I think there is a very easy solution. Notice that $\angle DKI=\angle DAI= \frac{\angle A}{2}$ and $\angle DIK =\angle DAF= \frac{\angle A}{2}.$ So, $DK=DI.$ Moreover, $KF^2=DK^2-DF^2$ and $IG^2=DI^2-DG^2$. Hence, we have $KF=IG.$ Now, by the law of sines in $\triangle KFL$ and $\triangle LGI$,

$$\frac{KL}{\sin \angle KFL}=\frac{KF}{\sin \angle KLF}, \\ \frac{LI}{\sin \angle LGI}=\frac{LI}{\sin \angle AGF}=\frac{IG}{\sin \angle GLI}.$$

Having $KF=IG$ and $\angle AGF=\angle KFL$, we are done.

Simple bisection geometry

2 Answers2