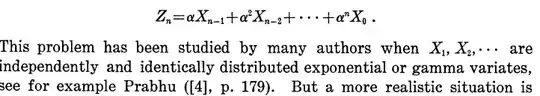Question
Let $Z_i\sim\chi_{(1)}^2\sim\Gamma(\frac{1}{2},\frac{1}{2})$ be i.i.d. chi-square random variables. We define: $$ W_n =\Bigl[\sum_{i = 1}^{n-1}\frac{Z_i}{2^{i}}\Bigr] + \frac{Z_n}{2^{n-1}} \mbox{ $\forall n\geq 2$} $$ For example: $W_2 = \frac{1}{2}Z_1+\frac{1}{2}Z_2$, $W_3 = \frac{1}{2}Z_1+\frac{1}{4}Z_2+\frac{1}{4}Z_3$ and so on.
I would like to determine the distribution of $W_{\infty}$ defined as: $$ W_{\infty} = \lim_{n\to\infty}W_n = \sum_{k = 1}^{\infty} \frac{Z_k}{2^{k}} \mbox{ where $Z_k\sim \Gamma\Bigl(\frac{1}{2},\frac{1}{2}\Bigr)$ are i.i.d.} $$ More specifically I have interest in computing the probability $P(W_{\infty} > 1$).
References
Note that this problem has references, in particular in this paper by Mathai:
Reference [4]:
In my case, following its notations $\alpha = \frac{1}{2}$, $X_i\sim\Gamma(\frac{1}{2},\frac{1}{2})$ are i.i.d. and $n\to\infty$. The main problem is that I didn't manage to find Prabhu's work about this fact, and in general I didn't manage to find any other references to this problem.
My attempt
I was trying to approach this problem using the Levy-criteria for the convergence in distribution.. in particular I was trying to calculate (since they are indipendent random variables) the infinite product of their characteristic functions, which is the characteristic function of $W_{\infty}$.. but I wasn't able to determine a closed form for it. In particular if $H_k \sim \Gamma(1/2,2^k)$ then $\phi_{H_k}(t) = \Bigl(1-\frac{t}{2^k}\Bigr)^{-\frac{1}{2}}$ and so: $$ \phi_{W_{\infty}}(t) = \prod_{k = 0}^{\infty}\frac{1}{\sqrt{1-\frac{it}{2^k}}} $$
Code and simulation
I'm sure that $W_n$ converges in distribution by simulating it using R, in particular the following code:
it = 10000
n = 300
mat = matrix(rep(0,n*it),n,it)
w = vector()
for(i in 1:n) {
mat[i,] = rchisq(it,1)
}
for(i in 1:n) {
mat[i,] = mat[i,]/2^i
}
for(j in 1:it) {
w[j] = sum(mat[,j])
}
hist(w,freq = F,breaks = seq(0,10,0.1))
produces the following output:
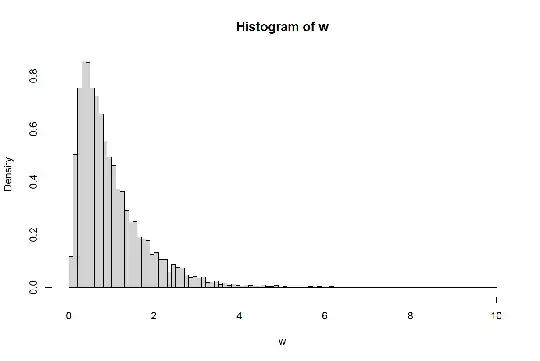$W_{300}$" />
which is the distribution of $W_{300}$. I don't really know if this is a well known distribution, and I don't really know if its density function has a closed form. I don't know how to proceed. Thank you in advance for your help!
New approximation of $P(W_{\infty} > 1)$
Using the software R and the library "CompQuadForm":
https://cran.r-project.org/web/packages/CompQuadForm/CompQuadForm.pdf
I manage to approximate the value of $P(W_{\infty} > 1)$ with the code:
library(CompQuadForm)
n = 10000
q = 1
lambda = vector()
for(i in 1:n) {
lambda[i] = 2^(-i)
}
acc1 = 10^(-15)
approx = davies(q, lambda, h = rep(1, length(lambda)), delta = rep(0,length(lambda)), sigma = 0, lim = 500000, acc = acc1)$Qq
sprintf("%.30f",approx)
which gives: $$ P(W_{\infty} > 1) \approx 0.371741079532780016592141691945 $$
which I think are the real first 30 digits. (I'm sure for the first 15 since I set an accuracy of $10^{-15}$). Of course I would prefer an "analytic" form of this number..
