When is this integral a polynomial?

Question

Consider the functions or integrals $f : \mathbb{R} \to \mathbb{R}$ of the form, $$ f(x) = \int_{a}^{b}K(|x-y|)u(y)dy $$ where $u$ is known and $K$ is a weakly singular kernel (or a continuous kernel for simplicity). How do we show that this function $f$ is a polynomial ? One approach would be to actually compute the integral, however, that is a difficult task. For example, consider the integral $$ \int_{-1}^{1} |x-y|^{-s}(1-y^2)^{\frac{1+s}{2}} dy = \frac{\pi (1+s)}{2\sin{\left( \pi\frac{1+s}{2} \right)}}(1-sx^2),$$ where $s \in (-1,1)$, $x\in[-1,1]$. Another approach would be to show higher order derivatives of this integral are zero, but that seems impossible because of the weakly singular kernel. Any hints?

P.S : I have not proven the integral above yet.

Edit : Maybe the question I have asked is too general. We can also start with the following problem: For what values of $s \in (0,1)$ is $$\int_{-1}^{1}(1-y^2)^s\ln{|x-y|}dy $$ a polynomial in $x$?

Edit 2 : It appears that above integral is a polynomial for $x\in[-1,1]$, $s=1/2$.

Answer 1

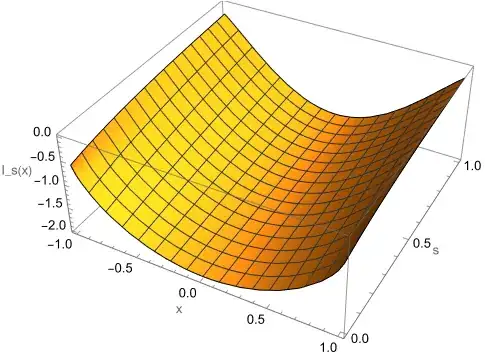
Clearly we have:

\begin{eqnarray} &&f_s(x):=\int\limits_{-1}^1 (1-y^2)^s \log|x-y| dy = \\ &&\int\limits_0^{1+x} (1-(x-y)^2)^s \log(y) dy + \int\limits_0^{1-x} (1-(x+y)^2)^s \log(y) dy % \end{eqnarray}

Now

\begin{eqnarray} f_s(0) &=& 2 \int\limits_0^1 (1-y^2)^2 \log(y) dy \\ &=& \frac{d}{d \theta} \frac{\Gamma(s+1) \Gamma(\theta/2+1/2)}{\Gamma(s/2+\theta/2+3/2)} |_{\theta=0} \\ &&\sqrt{\pi} \Gamma(1+s) \frac{\phi^{(0)}(1/2) - \phi^{(0)}(3/2+s)}{2 \Gamma(3/2+s)} \end{eqnarray}

As for the derivatives we write the following:

\begin{eqnarray} \left.\frac{d^n}{d x^n} f_s(x) \right|_{x=0} &=& \int\limits_0^1 \frac{d^n}{d x^n} \left( \left. \left(1-(x-y)^2\right)^s + \left(1-(x+y)^2\right)^s \right) \right|_{x=0} \log(y) dy + \mbox{additional terms}\\ \end{eqnarray}

There are two things that need to be pointed out. Firstly, for the calculation of the first term we will be using the Faa di Bruno formula with the external function being $x \rightarrow x^s$ and the internal function being equal to $x \rightarrow 1-(x+\epsilon y)^2$. Secondly, we will be arguing that the additional terms disappear (even though some of them are singular) as $x \rightarrow 0$. Thus we have:

\begin{eqnarray} \left.\frac{d^n}{d x^n} f_s(x) \right|_{x=0} &=& \\ &=& \sum\limits_{\epsilon=\pm} \sum\limits_{m_2=0}^{\lfloor n/2 \rfloor} \frac{n!}{(n-2 m_2)! m_2!} s_{(n-m_2)} (-1)^{m_2} (-2 \epsilon)^{n-2 m_2} \cdot \underline{\int\limits_0^1 (1-y^2)^{s-(n-m_2)} y^{n-2 m_2} \log(y) dy} \\ &=& \sum\limits_{\epsilon=\pm} \sum\limits_{m_2=0}^{\lfloor n/2 \rfloor} \frac{n!}{(n-2 m_2)! m_2!} s_{(n-m_2)} (-1)^{m_2} (-2 \epsilon)^{n-2 m_2} \cdot \left. \underline{\frac{\Gamma \left(\frac{n+1}{2}\right) \Gamma (s+1) \left(H_{\frac{n-1}{2}}-H_{\frac{n+1}{2}+s}\right)}{4 \Gamma \left(\frac{n+3}{2}+s\right)}} \right|_{s \rightarrow s-(n-m_2), n \rightarrow n-2 m_2 } \end{eqnarray}

The Mathematica code verifies the result:

{x} = RandomReal[{0, 1/10}, 1, WorkingPrecision -> 50]; M = 10;
s = RandomReal[{0, 1}, WorkingPrecision -> 50];
(*s=RandomInteger[{1,5}];*)
NIntegrate[(1 - (x - y)^2)^s Log[y], {y, 0, 1 + x}] + 
  NIntegrate[(1 - (y + x)^2)^s Log[y], {y, 0, 1 - x}];
Take[Accumulate@
   Join[{(Sqrt[[Pi]]
       Gamma[1 + s] (PolyGamma[0, 1/2] - PolyGamma[0, 3/2 + s]))/(
     2 Gamma[3/2 + s])}, 
    Table[Sum[
       n!/((n - 2 m2)! m2!)
         Pochhammer[s - (n - m2) + 1, n - m2] (-1)^
         m2 ((-2) (eps))^(n - 2 m2) (
        Gamma[(1 + n - 2 m2)/2] Gamma[
          1 + s - (n - m2)] (HarmonicNumber[1/2 (-1 + n - 2 m2)] - 
           HarmonicNumber[(1 + n - 2 m2)/2 + s - (n - m2)]))/(
        4 Gamma[(3 + n - 2 m2)/2 + s - (n - m2)]), {m2, 0, 
        Floor[n/2]}, {eps, -1, 1, 2}] x^n/n!, {n, 1, 
      M}]], -5] // MatrixForm
NIntegrate[(1 - y^2)^s Log[Abs[x - y]], {y, -1, 1}, 
 WorkingPrecision -> 30]

Now, to answer your question. First of all note that the following identity holds true:

\begin{eqnarray} &&\sum\limits_{\epsilon=\pm} \sum\limits_{m_2=0}^{\lfloor n/2 \rfloor} \frac{n!}{(n-2 m_2)! m_2 !} s_{(n-m_2)} (-1)^{m_2} (-2 \epsilon)^{n-2 m_2} \Gamma(\frac{1+n-2 m_2}{2}) \Gamma(1+s-(n-m_2)) \frac{ H_{\frac{1}{2}(-1+n-2 m_2)} - H_{\frac{1+n-2 m_2}{2}+s-(n-m_2)} }{4\Gamma(\frac{3+n-2 m_2}{2}+s-(n-m_2))} =\\ && (\frac{n}{2})! \frac{2^{n/2}}{(n-1)!!} (-1)^{n/2-1} 1_{n \% 2 == 0} (n-1)! \sqrt{\pi} \frac{\Gamma(s+1)}{\Gamma(s+3/2-n/2)} \frac{1}{\Gamma(1+n/2)} \end{eqnarray}

for $n=1,2,3,\cdots$. See Update 1 below for the derivation.

In[393]:= s = RandomReal[{0, 1}, WorkingPrecision -> 200]; M = 14;
l1 = Table[
   Sum[n!/((n - 2 m2)! m2!)
      Pochhammer[s - (n - m2) + 1, n - m2] (-1)^
      m2 ((-2) (eps))^(n - 2 m2) (
     Gamma[(1 + n - 2 m2)/2] Gamma[
       1 + s - (n - m2)] (HarmonicNumber[1/2 (-1 + n - 2 m2)] - 
        HarmonicNumber[(1 + n - 2 m2)/2 + s - (n - m2)]))/(
     4 Gamma[(3 + n - 2 m2)/2 + s - (n - m2)]), {m2, 0, 
     Floor[n/2]}, {eps, -1, 1, 2}], {n, 1, M}];
l2 = Table[(n/2)! 2^(n/2)/(n - 1)!! If[Mod[n, 2] == 0, (-1)^(n/2 - 1),
      0] (n - 1)! Sqrt[Pi] Gamma[
     s + 1] 1/(Gamma[s + 3/2 - n/2] Gamma[1 + n/2]), {n, 1, M}];
l1 - l2
Out[396]= {0.10^-200, 0.10^-199 + 0.10^-200 I, 
 0.10^-198 + 0.10^-200 I, 0.10^-197 + 0.10^-198 I, 
 0.10^-196 + 0.10^-197 I, 0.10^-196 + 0.10^-197 I, 
 0.10^-195 + 0.10^-196 I, 0.10^-195 + 0.10^-196 I, 
 0.10^-193 + 0.10^-194 I, 0.10^-193 + 0.10^-194 I, 
 0.10^-191 + 0.10^-192 I, 0.10^-191 + 0.10^-192 I, 
 0.10^-189 + 0.10^-189 I, 0.10^-189 + 0.*10^-189 I}

What I wrote here before was a wrong conclusion that those quantities become identically zero for $n$ big enough iff $s$ is a positive integer. This wrong conclusion was based on analysing the Pochhammer factor $s_{(n-m_2)}$ in the left hand side of the above identity. But what is more important is the Gamma function in the denominator of the left hand side! Indeed if we take $n$ even and $s$ positive half integer then for $n$ being large enough the argument of the Gamma function in the denominator becomes a negative integer and as such the Gamma function is infinity and the both sides are identically zero.

So in short, the quantity $f_s(x)$ becomes a polynomial iff $s$ is a positive half integer.

Update:

From the above it is actually not quite clear as to whether the higher derivatives of $f_s(x)$ exist. We will therefore show in a different way that they all do exist. Here we go:

\begin{eqnarray} f_s(x) &=& \int\limits_0^{1+x} (1-(x-y)^2)^s \log(y) dy + \int\limits_0^{1-x} (1-(x+y)^2)^s \log(y) dy \\ &=& \sum\limits_{n=0}^\infty \binom{s}{n} (-1)^n \sum\limits_{l=0}^{2 n} \binom{2n}{l} x^{2n-l} \left[ (-1)^l \int\limits_0^{1+x} y^l \log(y) dy + \int\limits_0^{1-x} y^l \log(y) dy \right] \\ &=& \sum\limits_{n=0}^\infty \binom{s}{n} (-1)^n \sum\limits_{l=0}^{2 n} \binom{2n}{l} x^{2n-l} \left[ (-1)^l \left. \frac{y^{1+l} \left(-1+(1+l) \log(y)\right) }{(1+l)^2} \right|_0^{1+x} + \left. \frac{y^{1+l} \left(-1+(1+l) \log(y)\right) }{(1+l)^2} \right|_0^{1-x} \right] \\ &=& \sum\limits_{n=0}^\infty \binom{s}{n} (-1)^n \sum\limits_{l=0}^{2 n} \binom{2n}{l} x^{2n-l} \left[ \right. \\ && \left. (-1)^{l+1} \frac{(1+x)^{l+1}}{(1+l)^2} + (-1) \frac{(1-x)^{l+1}}{(1+l)^2} + \right. \\ &&\left. (-1)^{l} \frac{(1+x)^{l+1}}{(1+l)^1} \log(1+x) + \frac{(1-x)^{l+1}}{(1+l)^1} \log(1-x) \right. \\ &&\left. \right] \end{eqnarray}

We clearly see that the expression in square brackets above is $C^\infty(x)$ for every $l=0,1,2,\cdots$ and as such the whole expression is $C^\infty(x)$ as expected.

Update 1:

By using the expression for the $n$th derivative as given in the answer below given by Claudio and then by using the Pfaff transformation for the Gaussian hypergeometric function we found the following neat closed form expression for the function in question:

\begin{eqnarray} f_s(x) &=& \sqrt{\pi} \Gamma(1+s) \frac{\phi^{(0)}(1/2) - \phi^{(0)}(3/2+s)}{2 \Gamma(3/2+s)} +\\ && \sum\limits_{n=1}^\infty \frac{2^n}{(2n-1)!!} (-1)^{n-1} (2n-1)! \sqrt{\pi} \frac{\Gamma(s+1)}{\Gamma(s+\frac{3}{2}-n)} \cdot \frac{x^{2n}}{(2n)!} \end{eqnarray}

{x} = RandomReal[{0, 1}, 1, WorkingPrecision -> 50]; M = 40;
s = RandomReal[{0, 1}, WorkingPrecision -> 50];
ll = Join[{(
    Sqrt[\[Pi]]
      Gamma[1 + s] (PolyGamma[0, 1/2] - PolyGamma[0, 3/2 + s]))/(
    2 Gamma[3/2 + s])}, Table[
     2^(n)/(2 n - 1)!! (-1)^(n - 1) (2 n - 1)! Sqrt[Pi] Gamma[
      s + 1] 1/(Gamma[s + 3/2 - n]) x^(2 n)/(2 n)!, {n, 1, M}]];
Take[Accumulate@ll, -5] // MatrixForm
NIntegrate[(1 - y^2)^s Log[Abs[x - y]], {y, -1, 1}, 
 WorkingPrecision -> 30]

From the above it clearly follows that the expression is indeed a polynomial in $x$ if and only if $s$ is a positive half-integer.

Answer 2

Assuming that \begin{eqnarray} &&I_s(x)=\int\limits_{-1}^1 (1-y^2)^s \log|x-y| dy \end{eqnarray} is a polynomial in $x$ for some $s \in (0,1)$, we expect the n-th derivative with respect to $x$ of $f_s(x)$ to be zero for some $n \geq 1$. Now, let $f_s(x,y) = (1-y^2)^s \log|x-y|$. The first derivative $D_{1}(x) = dI_s(x)/dx$ is \begin{eqnarray} &&D_1(x)=\int\limits_{-1}^1 \frac{\partial f_s(x,y)}{\partial x} dy = \int\limits_{-1}^1 \frac{(1-y^2)^s}{x-y}dy \end{eqnarray} and \begin{eqnarray} &&D_2(x)=\int\limits_{-1}^1 -\frac{(1-y^2)^s}{(x-y)^2}dy \end{eqnarray} \begin{eqnarray} &&D_3(x)=\int\limits_{-1}^1 2\frac{(1-y^2)^s}{(x-y)^3}dy \end{eqnarray} \begin{eqnarray} &&D_4(x)=\int\limits_{-1}^1 -6\frac{(1-y^2)^s}{(x-y)^4}dy \end{eqnarray} \begin{eqnarray} &&D_5(x)=\int\limits_{-1}^1 24\frac{(1-y^2)^s}{(x-y)^5}dy \end{eqnarray} which suggests \begin{align} D_n(x)&=(-1)^{n-1}(n-1)!\int\limits_{-1}^1 \frac{(1-y^2)^s}{(x-y)^n}dy \\ &= (-1)^{n-1}(n-1)! \sqrt{\pi } x^{-n} \Gamma (s+1) \, _2\tilde{F}_1\left(\frac{n}{2},\frac{n+1}{2};s+\frac{3}{2};\frac{1}{x^2}\right) \end{align} where $_2\tilde{F}_1(a,b;c;z)$ is the regularized hypergeometric function $_2{F}_1(a,b;c;z)/\Gamma(c)$. As far as I can see, this n-th derivative of $I_s(x)$ can't be zero for any $n\geq 1$ irrespective of the choice of $s$.

In a different approach, for $|x|\geq 1$ and $s>-1$, Mathematica gives \begin{eqnarray} &&I_s(x)=\int\limits_{-1}^1 (1-y^2)^s \log|x-y| dy \\ &&= \frac{\sqrt{\pi } \Gamma (s+1) \left(4 x^2 \log (x)-\Gamma \left(s+\frac{3}{2}\right) \, _3\tilde{F}_2\left(1,1,\frac{3}{2};2,s+\frac{5}{2};\frac{1}{x^2}\right)\right)}{4 x^2 \Gamma \left(s+\frac{3}{2}\right)} \end{eqnarray} which I can't see how possibly could be reduced to a polynomial in $x$.

[UPDATED]

Now, for $x\in(-1,1)$, \begin{eqnarray} &&I_{1/2}(x)=\int\limits_{-1}^1 (1-y^2)^{1/2} \log|x-y| dy \\ &&=\int\limits_{-1}^x (1-y^2)^{1/2} \log(x-y) dy + \int\limits_{x}^1 (1-y^2)^{1/2} \log(y-x) dy \end{eqnarray}

Let \begin{eqnarray} &&g(x,y)=\int\limits_{-1}^x (1-y^2)^{1/2} \log(x-y) dy \\ &&h(x,y)=\int\limits_{x}^1 (1-y^2)^{1/2} \log(y-x) dy \end{eqnarray}

Then \begin{eqnarray} &&I_{1/2}(x)=\lim_{y \to x^-}g(x,y) - \lim_{y \to -1^+}g(x,y) + \lim_{y \to 1^-}h(x,y) - \lim_{y \to x^+}h(x,y) \\ \end{eqnarray} Both $\lim_{y \to x^-}g(x,y) = \lim_{y \to x^+}h(x,y) = +\infty$ so, in the sense of a principal value integral, the real part of $I_{1/2}(x)$ is \begin{eqnarray} &&\mathrm{Re}\{\mathrm{PV}[I_{1/2}(x)]\}=\mathrm{Re}\{\lim_{y \to 1}h(x,y) - \lim_{y \to -1}g(x,y)\} \\ &&=\frac{\pi}{4} \left(2 x^2-1-\log (4)\right) \end{eqnarray} (the above result also includes a term $-2 \Im\left(\text{Li}_2\left(-x-i \sqrt{1-x^2}\right)-\text{Li}_2\left(x-i \sqrt{1-x^2}\right)+\text{Li}_2\left(i \sqrt{1-x^2}-x\right)-\text{Li}_2\left(x+i \sqrt{1-x^2}\right)\right)$

whose real part sum up to zero.)

Although I didn't have explored other values of $s$, a numerical analysis suggests $I_s(x)$ can be expressed as a polynomial in $x$ for $x\in (-1,1)$ and all $s\in (0,1)$.

Answer 3

Now, let us do the original integral from the body of the question.

\begin{eqnarray} &&\int\limits_{-1}^{+1} \left| x - y \right|^{-s} \cdot \left( 1- y^2 \right)^{\frac{1+s}{2}} dy = \\ &&\int\limits_0^{1+x} y^{-s} \cdot \left( 1 - (x-y)^2 \right)^{\frac{1+s}{2}} dy + \int\limits_0^{1-x} y^{-s} \cdot \left( 1 - (x+y)^2 \right)^{\frac{1+s}{2}} dy = \\ && \sum\limits_{l=0}^\infty \sum\limits_{p=0}^{2 l} \binom{\frac{1+s}{2}}{l} (-1)^l \binom{2 l}{p} x^{2l-p} \left[ (-1)^p \frac{y^{p-s+1}}{p-s+1} |_{0}^{1+x} + \frac{y^{p-s+1}}{p-s+1} |_{0}^{1-x} \right] = \\ && \sum\limits_{l=0}^\infty \sum\limits_{p=0}^{2 l} \binom{\frac{1+s}{2}}{l} (-1)^l \binom{2 l}{p} x^{2l-p} \left[ (-1)^p \frac{(1+x)^{p-s+1}}{p-s+1} + \frac{(1-x)^{p-s+1}}{p-s+1} \right] = \\ && \sum\limits_{l=0}^\infty \sum\limits_{p=0}^{2 l} \sum\limits_{m=0}^\infty \binom{\frac{1+s}{2}}{l} (-1)^l \binom{2 l}{p} \frac{1}{p-s+1} \binom{p-s+1}{m} \left[(-1)^p + (-1)^m \right] x^{2l-p+m} \underbrace{=}_{2l-p \rightarrow p} \\ && \sum\limits_{l=0}^\infty \sum\limits_{p=0}^{2 l} \sum\limits_{m=0}^\infty \binom{\frac{1+s}{2}}{l} (-1)^l \binom{2 l}{p} \frac{1}{2l-p-s+1} \binom{2l-p-s+1}{m} \left[(-1)^p + (-1)^m \right] x^{p+m} \underbrace{=}_{m+p\rightarrow m} \\ && \sum\limits_{m=0}^\infty \left[ 1 + (-1)^m \right] x^m \sum\limits_{l=0}^\infty \binom{\frac{1+s}{2}}{l} (-1)^l \sum\limits_{p=0}^{2 l \wedge m} \binom{2 l}{p} \frac{1}{2l-p-s+1} \binom{2l-p-s+1}{m-p} (-1)^p = \\ && \sum\limits_{m=0}^\infty \left[ 1 + (-1)^m \right] x^m \sum\limits_{l=0}^\infty \binom{\frac{1+s}{2}}{l} (-1)^l \frac{(-1)^{1+m} (-1+m+s)!}{(-1-2 l+m+s) m! (-1+s)!} = \\ && \sum\limits_{m=0}^\infty \left[ 1 + (-1)^m \right] x^m \frac{(-1)^{1+m} \Gamma(\frac{1}{2}(1-m-s)) \Gamma(\frac{3+s}{2}) (-1+m+s)!}{2 \Gamma(\frac{4-m}{2}) m! (-1+s)!} \underbrace{=}_{m \rightarrow 2 m} \\ && \sum\limits_{m=0}^\infty x^{2 m} \frac{(-1)^{1+2m} \Gamma(\frac{1}{2}(1-2m-s)) \Gamma(\frac{3+s}{2}) (-1+2m+s)!}{ \Gamma(2-m) (2 m)! (-1+s)!} = \\ && (-1)^{1} \frac{\Gamma(\frac{3+s}{2})}{(-1+s)!} \sum\limits_{m=0}^1 x^{2 m} \frac{\Gamma(\frac{1}{2}(1-2m-s)) (-1+2m+s)!}{ \Gamma(2-m) (2 m)! } \\ && \frac{\Gamma(\frac{3+s}{2})}{(-1+s)!} \left[ \frac{\Gamma(\frac{1}{2}(1-s)) (-1+s)!}{ 1 } + \frac{\Gamma(\frac{1}{2}(1-2-s)) (-1+2+s)!}{ 2! } \cdot x^2 \right] \\ &&\frac{\pi (1+s)}{2 \sin[\pi (1+s)/2]} \left(1-s x^2 \right) \end{eqnarray}

Update:

By generalizing the approach above we found the following identity:

\begin{eqnarray} f^{(u)}_s(x):=\int\limits_{-1}^1 \left| x - y \right| ^{-s} \cdot u(y^2) dy = \sum\limits_{m=0}^\infty x^{2 m} \cdot \int\limits_0^1 v^{-\frac{1}{2} - m - \frac{s}{2}} u(v) dv \cdot \frac{ (-1+2 m+s)!}{(2m)! (-1+s)!} \end{eqnarray}

In particular if the function $u(v)$ is a polynomial $u(v) := \sum\limits_{j=0}^{\cdots} c_j v^j$ then we have: \begin{eqnarray} f^{(u)}_s(x):= \sum\limits_{m=0}^\infty x^{2 m} \left( \sum\limits_{j=0}^{\cdots} \frac{2 c_j}{s+2 m-2 j-1}\right) \cdot \frac{(-1) (-1+2 m+s)!}{(2m)! (-1+s)!} \end{eqnarray}

In[1105]:= 
M = 20;
{c1, c2, c3, c4} = RandomReal[{0, 2}, 4, WorkingPrecision -> 50];
u[y_] := c1 + c2 y + c3 y^2 + c4 y^3;
{x, s} = RandomReal[{0, 1}, 2, WorkingPrecision -> 50];
Take[Accumulate@
  Table[x^(2 m) (2 (c4/(-7 + 2 m + s) + c3/(-5 + 2 m + s) + 
        c2/(-3 + 2 m + s) + c1/(-1 + 2 m + s))) (-1) (-1 + 2 m + 
        s)!/((2 m)! (-1 + s)!), {m, 0, M}], -5]
NIntegrate[Abs[x - y]^(-s) u[y^2], {y, -1, +1}, WorkingPrecision -> 20]
Out[1109]= {6.732240551929893598998843563293131173142318189915, 

6.732240532870031910465627488919415982663760660392, 

6.732240524499490895052383960180218671612761950458, 

6.732240520799152621695056636305660295491681772765, 

6.732240519153768098655950357463278334828043213758}
Out[1110]= 6.7322405178151331850

Finally , if we take $u(y) := (1-y)^\alpha$ then we have:

\begin{eqnarray} f^{(u)}_s(x):= \sum\limits_{m=0}^\infty x^{2 m} \frac{(-2) \Gamma(1+\alpha) \Gamma(\frac{1}{2}(3-2 m-s)) (-2+2 m+s)!}{\Gamma(\frac{1}{2}(3+2 \alpha-2 m-s)) (2m)! (-1+s)!} \end{eqnarray}

which reduces to a polynomial if and only if $3+2 \alpha - s$ is an even positive integer.

In[1143]:= 
M = 20;
{alpha} = RandomReal[{0, 2}, 1, WorkingPrecision -> 50];
u[y_] := (1 - y)^alpha;
{x, s} = RandomReal[{0, 1}, 2, WorkingPrecision -> 50];
Take[Accumulate@
  Table[x^(2 m) (((-2) Gamma[1 + alpha] Gamma[
       1/2 (3 - 2 m - s)] (-2 + 2 m + s)!)/(
     Gamma[1/2 (3 + 2 alpha - 2 m - s)] (2 m)! (-1 + s)!)), {m, 0, 
    M}], -5]
NIntegrate[Abs[x - y]^(-s) u[y^2], {y, -1, +1}, WorkingPrecision -> 20]
Out[1147]= {1.9031964634459376578194552965277491310931519103027 + 
  0.10^-50 I, 
 1.9031964634456814521855812677359334453451112741067 + 0.10^-50 I, 
 1.9031964634456074747778039034162966105864223312437 + 0.10^-50 I, 
 1.9031964634455859522475540218908289574174841772217 + 0.10^-50 I, 
 1.9031964634455796481009684753117068942042459546364 + 0.*10^-50 I}
Out[1148]= 1.9031964634455770059

Answer 4

Here is the derivation of the sum identity:

\begin{eqnarray} &&\sum\limits_{p=0}^{(2l) \wedge m} \binom{2 l}{p} \binom{2l-p-s+1}{m-p} \frac{(-1)^p}{2l-p-s+1} = \\ &&\sum\limits_{p=0}^{(2l) \wedge m} \binom{2 l}{p} (-1)^{m-p} \binom{m-2l+s-2}{m-p} \frac{(-1)^p}{2l-p-s+1} = \\ &&\left.(-1)^{m+1} \sum\limits_{p=0}^{l_1 \wedge m} \binom{l_1}{p} \binom{l_2}{m-p} \frac{1}{A+p}\right|_{l_1=2 l,l_2=m-2l+s-2,A=s-2l-1} = \\ &&\left.(-1)^{m+1} \binom{l_2}{m} \frac{1}{A} F_{3,2} \left[ \begin{array}{lll} A & -l_1 & -m \\ A+1 &l_2-m+1 \end{array}; 1 \right]\right|_{l_1=2 l,l_2=m-2l+s-2,A=s-2l-1} =\\ &&\left.(-1)^{m+1} \binom{l_2}{m} \frac{1}{A} F_{2,1} \left[ \begin{array}{lll} -l_1 & -m \\ A+1 \end{array}; 1 \right]\right|_{l_1=2 l,l_2=m-2l+s-2,A=s-2l-1} =\\ && \left.(-1)^{m+1} \binom{l_2}{m} \frac{1}{A} \frac{\Gamma(A+1) \Gamma(A+1+l_1+m) }{\Gamma(A+1+l_1) \Gamma(A+1+m)} \right|_{l_1=2 l,l_2=m-2l+s-2,A=s-2l-1} =\\ && \left.(-1)^{m+1} \binom{l_2}{m} \frac{1}{A} \frac{s^{(m)}}{(s-2 l)^{(m)}}\right|_{l_1=2 l,l_2=m-2l+s-2,A=s-2l-1} =\\ && (-1)^{m+1} \frac{(m+s-2l-2)!}{m!(s-2l-2)!} \frac{1}{s-2l-1} \frac{s^{(m)}}{(s-2 l)^{(m)}} = \\ && (-1)^{m+1} \frac{(m+s-2l-2)!}{m!(s-2l+m-1)!} s^{(m)} \\ && (-1)^{m+1} \frac{1}{m!(s-2l+m-1)} s^{(m)} \\ && (-1)^m \frac{s^{(m)}}{m!} \cdot \frac{1}{-s+2l-m+1} \end{eqnarray}

In the second line we used the identity $\binom{n}{k} = (-1)^k \binom{k-n-1}{k} $. The third line is obvious. The forth line follows from taking out the $p=m$ term and expressing the rest as a hypergeometric function. The fifth line follows the coincidence that $A= l_2-m+1$. The sixth line uses the Gauss' summation theorem. the rest are just simplifications.