Analytic extension of $\text{Li}_0^{(1,0)}(z):=-\displaystyle\sum_{n=1}^{\infty}\ln(n)z^{n}$ for $|z|>1$

Question

I would like to extend the domain of the following function:

$$\text{Li}_0^{(1,0)}(z):=-\sum_{n=1}^{\infty}\ln(n)z^{n}\qquad\text{where }|z|<1$$

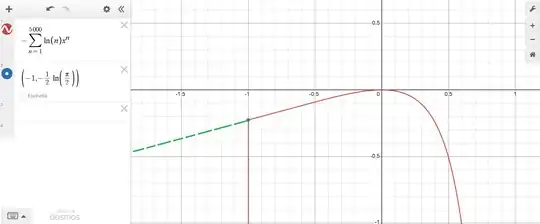
The part in red is the series, the part in green is a hypothetical extension

I'll start by saying that I don't know any techniques for doing something like this, so any advice (links, names of theorems or similar) is useful.

I could only find the value in $x=-1$

$$\text{Li}_0^{(1,0)}(-1)=\lim_{s\to 0}\left[ \sum_{n=1}^{\infty} \frac{(-1)^n\ln(n)}{n^s}\right] = -\frac{1}{2}\ln\left(\frac{\pi}{2}\right)$$

I've searched for possible representations on Wolfram, but none include the one with $\nu=0$

Unfortunately I found the integral representation of polylogarithms $\text{Li}_{\nu}(z)$ only for $\Re(\nu)>0$

From a computational point of view a series is heavier than an integral, so I was wondering if it was possible to represent $$\text{Li}_{0}^{(1,0)}(z):=\left.\frac{\partial}{\partial\nu}\text{Li}_{\nu}(z)\right|_{\nu=0}$$ without using infinite sums or products.

the only formula I've found that include zero is this:

$$\text{Li}_{\nu}(z) = -\frac{i}{2 π} \int_{-i ∞ + γ}^{i ∞ + γ} (-t)^{1 - \nu} (-z)^{-t} Γ(-t) Γ(t) \mathrm{d}t$$ $$\text{ for }(-1<γ<0\text{ and }z\neq 0\text{ and }(\text{arg}(-z)<π\text{ or }\Re(\nu)>1))$$

So

$$\text{Li}^{(1,0)}_{\nu}(z) = \frac{i}{2 π} \int_{-i ∞ + γ}^{i ∞ + γ} (-t)^{1 - \nu}\ln(-t) (-z)^{-t} Γ(-t) Γ(t) \mathrm{d}t$$ $$\text{Li}^{(1,0)}_{0}(z) = -\frac{i}{2 π} \int_{-i ∞ + γ}^{i ∞ + γ} \ln(-t) (-z)^{-t} Γ(-t) Γ(t+1) \mathrm{d}t$$ $$\text{Li}^{(1,0)}_{0}(z) = \frac{i}{2} \int_{-i ∞ + γ}^{i ∞ + γ} \ln(-t) (-z)^{-t} \csc(\pi t) \mathrm{d}t$$

But with this function I would also like to work with graphs and I don't use programs that know how to manage this type of representations with complex numbers.

Would anyone be able to suggest an alternative method to represent it?

Update 1

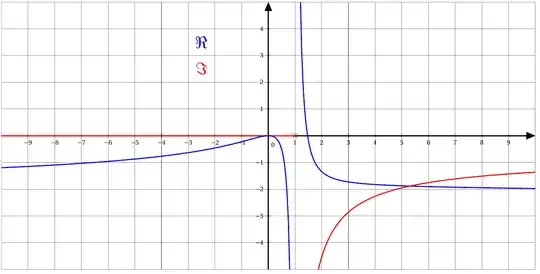
The graph is something like this:

Update 2

I obtained the following property: $$\Re\left[\text{Li}_0^{(1,0)}\left(e^{2\pi i x}\right)\right]=-\frac{1}{2}\left(\gamma+\ln\left(2\pi\right)+\frac{\psi\left(x\right)+\psi\left(1-x\right)}{2}\right)\qquad\text{for } 0<x<1$$

Hence also the following formulas for $n\geq 1$: $$\begin{align}\Re\left[\text{Li}_{-2n}^{(1,0)}\left(e^{2\pi i x}\right)\right]&=&\frac{(-1)^{n-1}}{(2\pi)^{2n}}\frac{\psi^{(2n)}\left(x\right)+\psi^{(2n)}\left(1-x\right)}{4}\\\Im\left[\text{Li}_{-(2n-1)}^{(1,0)}\left(e^{2\pi i x}\right)\right]&=&\frac{(-1)^{n-1}}{(2\pi)^{2n-1}}\frac{\psi^{(2n-1)}\left(x\right)-\psi^{(2n-1)}\left(1-x\right)}{4}\end{align}$$

Answer 1

For any $g$ analytic in $\Re s >0$ and (at most) of polynomial growth, if we define $G(z)=\sum_{ n \ge 1}g(n)z^n$ originally convergent in the unit disc by the growth assumption on $g$, then we have for $y \in \mathbb C -[0, \infty)$ the Lindelof representation $$G(y)=-\frac{1}{2\pi i}\int_{(1/2)}g(s)(-y)^s\frac{\pi ds}{\sin \pi s} \tag 1$$ which shows that the function can be analytically continued to $\mathbb C -[1, \infty)$

The proof is almost trivial since $(1)$ clearly defines an analytic function on $\mathbb C -[0, \infty)$ as for any $y$ in a compact set $K$ avoiding $[0, \infty)$ we have $\arg (-y) \in [-\pi+\delta, \pi-\delta]$ so $|\Re (1/2+it)\log (-y)= \log |y|/2-t\arg (-y)$ hence $|y^s|=O(\sqrt {|y|}e^{|t|(\pi/2-\delta)})$, while $|\frac{\pi}{\sin \pi s}|= O(e^{-\pi|t|/2})$ and $|g(s)|=O(|s|^k)$ by assumption, giving the normal (absolute and uniform on $K$) convergence of the integral, hence the analyticity of $G$

If now $y=-r, 0<r<1$ we can apply the residue theorem to move the line of integration to $N+1/2+i\infty$ and get that $G(-r)-\sum_{n \le N}g(n)(-r)^n=-\frac{1}{2\pi i}\int_{(N+1/2)}g(s)r^s\frac{\pi ds}{\sin \pi s} $ and trivially $r^{N+1/2+it} \to 0, N \to \infty$ so letting $ N \to \infty$ by dominated convergence we get $G(-r)=\sum_{ n \ge 1}g(n)(-r)^n$ and by the identity theorem we are done

In particular, with $g(s)=\log s$ we get the continuation of the OP function and more generally of any kind of dilogarithm $Li_{\alpha,r}=\sum_{n \ge 2}(\log n)^r\frac{z^n}{n^{\alpha}}$ where $r$ can be taken real if we modify a little $1$ so we take the integral on $3/2$ say - for $r=1,2,..$ of course $\log^r s$ is defined on $\Re s >0$ but for $r$ real general we need to define it on $\Re s >1$ so $\Re \log s >0$ hence $(\log s)^r$ is well defined

Then the asymptotics of $Li_{\alpha,r}$ are well known and one place to start looking at them is in the paper by Flajolet on Singularity Analysis and Asymptotics of Bernoulli Sums and reference from there

Answer 2

For all $z \in \mathbb{C}$ except $z$ real and greater than or equal to $1$, $\operatorname{Li}_{0}^{(1,0)}(z) $ has the integral representation $$\operatorname{Li}_{0}^{(1,0)}(z) = \frac{z \gamma}{1-z} + z \int_{0}^{\infty} \frac{\ln(x) e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx, $$ where $\gamma$ is the Euler-Mascheroni constant.

To prove this, all we need is the Bose-Einstein integral $$\operatorname{Li}_{s}(z) = \frac{z}{\Gamma(s)} \int_{0}^{\infty} \frac{x^{s-1}}{e^{x}-z} \, \mathrm dx,$$ which is valid for $\Re(s) >0$ and all complex values of $z$ except $z$ real and greater than or equal to $1$.

Integrating by parts, we have $$\operatorname{Li}_{s}(z) = \frac{z}{s \Gamma(s) }\int_{0}^{\infty} \frac{x^{s}e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx =\frac{z}{\Gamma(s+1)} \int_{0}^{\infty} \frac{x^{s}e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx, $$ which gives us (by analytic continuation) an integral representation for $\operatorname{Li}_{s}(z)$ for $\Re(s) >-1$.

Then differentiating both sides of the above equation with respect to $s$, we get

$$\operatorname{Li}_{s}^{(1,0)}(z) = -\frac{z \psi(s+1)}{\Gamma(s+1)} \int_{0}^{\infty} \frac{x^{s}e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx + \frac{z}{\Gamma(s+1)} \int_{0}^{\infty} \frac{x^{s}\ln(x) e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx, $$ where $\psi$ is the digamma function.

At $s=0$ this becomes $$ \begin{align} \operatorname{Li}_{0}^{(1,0)}(z) &= z \gamma \int_{0}^{\infty} \frac{e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx + z \int_{0}^{\infty} \frac{\ln(x)e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx \\ &= \frac{z \gamma}{1-z} + z \int_{0}^{\infty} \frac{\ln(x)e^{x}}{(e^{x}-z)^{2}} \, \mathrm dx. \end{align}$$

---

Let's check that we get the value $- \frac{\mathrm d}{\mathrm ds}\eta(s)\bigg|_{s=0} = -\frac{1}{2} \ln \left(\frac{\pi}{2} \right) $ for $z=-1$.

$$ \begin{align} \operatorname{Li}_{0}^{(1,0)}(-1) &= -\frac{\gamma}{2} - \int_{0}^{\infty} \frac{\ln(x) e^{x}}{(e^{x}+1)^{2}} \, \mathrm dx \\ &= -\frac{\gamma}{2} - \frac{1}{4} \int_{0}^{\infty} \frac{\ln(x)}{\cosh^{2} \left(\frac{x}{2} \right)} \, \mathrm dx \\ &= -\frac{\gamma}{2} - \frac{1}{2} \int_{0}^{\infty} \frac{\ln(2u)}{\cosh^{2} (u)} \, \mathrm du \\&= -\frac{\gamma}{2} - \frac{\ln(2) }{2} \int_{0}^{\infty} \frac{1}{\cosh^{2}(u)} \, \mathrm du - \frac{1}{2} \int_{0}^{\infty} \frac{\ln(u)}{\cosh^{2}(u)} \, \mathrm du \\&\overset{\spadesuit}{=} -\frac{\gamma}{2} - \frac{\ln(2)}{2}(1) - \frac{1}{2} \left(\ln \left(\frac{\pi}{4} \right) -\gamma \right) \\&=- \frac{1}{2} \ln \left(\frac{\pi}{2} \right) \end{align}$$

---

$\spadesuit$ Integral $\int_0^{\infty} \frac{\log x}{\cosh^2x} \ \mathrm{d}x = \log\frac {\pi}4- \gamma$

---

You can integrate by parts a second time to get an integral representation for $\operatorname{Li}_{s}(z)$ valid for $\Re(s) >-2$:

$$\operatorname{Li}_{s}(z) = \frac{z}{\Gamma(s+2)} \int_{0}^{\infty} \frac{x^{s+1} e^{x}(e^{x}+z)}{(e^{x}-z)^{3}} \, \mathrm dx. $$

Answer 3

Let $$\Psi_n(t,\nu):=B_n\left(\ln(t)-\psi(\nu),-\psi^{(1)}(\nu),...,-\psi^{(n-1)}(\nu)\right)$$ Where

• $\psi^{(n)}(z)$ is the polygamma function
• $B_n(x_1,...,x_n)$ the complete Bell polynomial.

---

$$\text{Li}^{(n,0)}_{\nu}(z)=\int_{0}^{\infty}\frac{t^{\nu+s-1}}{\Gamma(\nu+s)}\text{Li}_{-s}\left(ze^{-t}\right)\Psi_n(t,\nu+s)\mathrm{d}t\qquad {\Re(\nu)+s>0\atop s=1,2,3,...}$$

---

In particular, I can map $\nu\mapsto -\nu$, choose $\nu\geq 0$ and $n=1$ and $s$ such that $\nu-s=1$

$$\begin{align*} \text{Li}^{(1,0)}_{-\nu}(z)=&\int_{0}^{\infty}\text{Li}_{-\nu-1}\left(ze^{-t}\right)(\gamma+\ln(t))\mathrm{d}t\\ =&\int_{0}^{1}\left[\text{Li}_{-\nu}(z)-\frac{\text{Li}_{-\nu}(zs)}{s}\right]\frac{1}{\ln(s)}\mathrm{d}s&\nu\geq 0 \end{align*} $$