Need an intuitive example for how "P is necessary for Q" means "Q$\implies$P"?

Question

I am confused about how "P is necessary for Q" means "Q$\implies$P" (source: Kenneth Rosen DMGT).

Intuitively, I interpret "P is necessary for Q" as "for Q to happen, P must happen", which I basically feel is equivalent to "if P happens then Q must occur", i.e, "P $\implies$ Q". Could someone correct my understanding?

Answer 1

I think this is an intuitive example:

Suppose that it is necessary to have a ticket ($P$) in order to board a certain train ($Q$). That is, if you board the train ($Q$), then you have a ticket ($P$).

(It is not true that if you have a ticket ($P$) then you boarded the train ($Q$)! You might have a ticket and fail to board, or you might have a ticket and be refused boarding because you would not extinguish your cigarette.)

Answer 2

I interpret P is necessary for Q as for Q to happen, P must happen, which I basically feel is equivalent to if P happens then Q must occur, i.e., P ⟹ Q.

1. You were likely thrown off by erroneously framing P and Q as events that “happen/occur” and by the phrasing “for Q to happen”, which sounds like “to cause Q to follow or become true”, which in turn might sound like “implies Q”.

   However, P and Q are of course just statements, and we are just interrogating their binary truth values, rather than discussing chronology or causation.

2. P is necessary for Q can be rewritten as P being true is necessary for Q to be true, which can be rephrased as Q being true requires P to be true, which means that knowing that Q is true tells us that P is true, i.e., Q ⟹ P. (In yet other words: Q is sufficient for P.)

   Equivalently, P is necessary for Q can be rewritten as for Q to be true, P must be true, that is, for Q to be true, P cannot be false, which means that knowing that P is false tells us that Q is false, i.e., ¬P ⟹ ¬Q.

3. Thus, for example,

   • persistence is necessary for success (i.e., success ⟹ persistence)

   should be understood not as

   • ❌ persistence results in success,

   or even as

   • ❌ success results in persistence,

   but as

   • ✔️ success is evidence of persistence.

   To put it another way:

   • persistence is necessary for success (i.e., success ⟹ persistence)

   most assuredly means

   • if got no persistence, then surely got no success,

   which is logically equivalent to

   • ✔️ if got success, then surely got persistence.

Answer 3

You need to understand that the material conditional is not saying anything about temporal or causal relationships ... it merely says that 'if this is true, then that is true'

Consider:

"In order to take Calculus II ($II$), it is necessary that you take Calculus I ($I$). "

Temporally you might think $I \to II$, but that is not right: I can take Calculus I without taking Calculus II. But what we do have is $II \to I$: if it is true that I take (or have taken) Calculus II, then we can infer that I must have taken Calculus I.

Answer 4

To get the intuitive idea you can think of it in simple logic, and avoid symbols:

$ Q \Rightarrow P $ means that at every single case that $Q$ holds, then $P$ will certainly hold as well. So there is not even a single case in which $Q$ holds but $P$ doesn't. So $P$ is necessary for $Q$, as it always holds given the fact that $Q$ holds. Or in other words, $Q$ cannot hold, if $P$ doesn't hold. That's what makes $P$ necessary for $Q$.

Answer 5

Another intuitive example: If it is raining ($R$), then this it is cloudy ($C$). In classical propositional logic this simply rules out the possibility that, currently, it is raining and not cloudy.

$~~~~~~ R \implies C ~\equiv ~ \neg (R \land \neg C)$

The truth table for $R \implies C$:

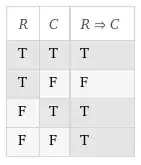
Suppose $R \implies C$ is true (lines 1, 3 or 4). Then, from the truth table, we have:

1. When $R$ is true (line 1), $C$ is true, i.e. $R$ is sufficient for $C$.

2. When $C$ is false (line 4), $R$ is false, i.e. $C$ is necessary for $R$.

Note that cloudiness ($C$) is not sufficient for rain ($R$). As is clear from the above truth table, when $C$ is true, the truth value of $R$ is indeterminate as you would expect.

---

Text version truth table:

R C R=>C

T T T

T F F

F T T

F F T

Answer 6

Consider that $(A\implies B)\Longleftrightarrow (\neg B\implies \neg A)$, so that it is necessary for $B$ to be true in order that $A$ might be true. For example, let $A$ denote that $x$ is a natural number and $B$ denote that $x$ is a real number. Clearly $A\implies B$ because every natural number is a real number. But if $x$ is not a real number, then it is certainly not a natural number: it is necessary that $x$ be real for it to possibly be natural, and so $B$ is necessary for $A$.

On the other hand, if $A\implies B$, then $A$ is sufficient for $B$: it is sufficient that $x$ be a natural number for it to be a real number.