0

Let $k$ be a field of characteristic zero and let $A \in k^{m \times n}$, $B \in k^{n \times m}$.

There are several posts in MSE asking for a proof for claim 1: $\operatorname{rank}(AB) \leq \min\{\operatorname{rank}(A), \operatorname{rank}(B)\}$, where the product is defined, so $B$, more generally, belongs to $k^{n \times p}$.

Question 1: Is claim 1 valid over any field of zero characteristic? (not just $\mathbb{R}$ or $\mathbb{C}$).

Then we can consider the special case where $B=A^T$.

For this special case there are posts asking for a proof for claim 2: $\operatorname{rank}(A) = \operatorname{rank}(AA^T) = \operatorname{rank}(A^TA)$.

It was mentioned here that this equality holds over $\mathbb{R}$ but not over $\mathbb{C}$, with the following counterexample: $ A= \begin{pmatrix} 1 & i \\ 0 & 0 \end{pmatrix} $, $A^T = \begin{pmatrix} 1 & 0 \\ i & 0 \end{pmatrix}$. Here $AA^T=\begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}$ and $A^TA=\begin{pmatrix} 1 & i \\ i & -1 \end{pmatrix}$. Here $\operatorname{rank}(A)=\operatorname{rank}(A^T)=1$, $\operatorname{rank}(AA^T)=0$, $\operatorname{rank}(A^TA)=1$.

We see that claim 1 holds, while claim 2 does not hold in general.

If claim 1 is valid over any zero characteristic field, then in particular we have claim 3: $\operatorname{rank}(AA^T) \leq \operatorname{rank}(A)$ and $\operatorname{rank}(A^TA) \leq \operatorname{rank}(A)$ (if it is true that $\operatorname{rank}(A) = \operatorname{rank}(A^T)$).

I have constructed $A \in \mathbb{C}(x,y)^{4 \times 2}$ of rank $2$ such that $AA^T \in \mathbb{C}(x,y)^{4 \times 4}$ is of rank $\geq 3$, which would contradict claim 3! This was a surprise. I wonder what will go wrong in a proof over a zero characteristic field different from $\mathbb{R}$ or $\mathbb{C}$. I will present the counterexample later; wishes to check again if I have no errors in my calculations.

See also this question.

Thank you very much!

Please tell me where is my error: $k=\mathbb{C}(x,y)$.

$A=\begin{pmatrix} 2x+1 & 2y \\ -2y & -2x \\ 2x & 2y \\ -26 & -2x+1 \end{pmatrix}$.

$A$ has rank two, since $\begin{pmatrix} 2x+1 & 2y \\ -2y & -2x \end{pmatrix}$ is invertible over $\mathbb{C}(x,y)$: the determinant is $-2x-4x^2+4y^2$.

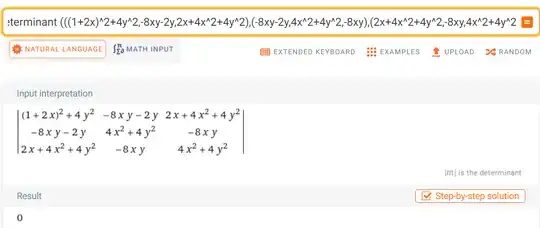
I now see that I had an error in my calculation, and the $3 \times 3$ minor of $AA^T$ I was considering has zero determinant... enter image description here

I really apologize.. Thank you very much for your help, it was good to make sure that claim 1 holds over any field (hence also claim 3).

user26857
  • 53,190
user237522
  • 7,263
  • 2
    The first claim is true over all fields. The characteristic of the field is irrelevant. As for your supposed counterexample to the third claim, would you please exhibit it? – user1551 Oct 05 '23 at 21:20
  • @user1551, thank you for your comment. I will exhibit the counterexample in an half an hour. – user237522 Oct 05 '23 at 21:21
  • 2
    (i) row rank = column rank holds over any field and (ii) $\text{rank}\big(AB)\leq \text{rank}\big(A)$ holds over any field since the former is in the column space of the latter. Thus claim 1 holds over any field. – user8675309 Oct 05 '23 at 21:21
  • @user8675309, thank you. – user237522 Oct 05 '23 at 21:22

2 Answers2

2

The inequality holds over any field, regardless of characteristic.

If $M$ is an $r\times s$ matrix with coefficients in the field $k$, then the rank of $M$ is the dimension of the range of $M$, viewed as a linear transformation $k^s\to k^r$.

If $A$ is an $n\times m$ matrix and $B$ is an $m\times p$ matrix, then the range of $AB$ is contained in the range of $A$; which gives $\mathrm{rank}(AB)\leq\mathrm{rank}(A)$. As for $\mathrm{rank}(AB)\leq \mathrm{rank}(B)$, this follows from the Rank-Nullity Theorem (which holds over any field): the rank of $AB$ is equal to $p-\dim(\mathbf{N}(AB))$. The rank of $B$ is $p-\dim(\mathbf{N}(B))$. Since $\mathbf{N}(B)\subseteq \mathbf{N}(AB)$, we have $\dim(\mathbf{N}(B))\leq \dim(\mathbf{N}(AB))$, so $$\begin{align*} \mathrm{rank}(AB) &= p-\dim(\mathbf{N}(AB))\\ &\leq p-\dim(\mathbf{N}(B))\\ &= \mathrm{rank}(B). \end{align*}$$ Since $\mathrm{rank}(AB)\leq \mathrm{rank}(A)$, and $\mathrm{rank}(AB)\leq\mathbf{rank}(B)$, you conclude $\mathbf{rank}(AB)\leq\min(\mathrm{rank}(A),\mathrm{rank}(B))$.

Note that nothing in the above proof uses the characteristic of $k$.

While claim 2 does not follow for $\mathbb{C}$, the corresponding claim is that $\mathrm{rank}(A)=\mathrm{rank}(AA^*) = \mathrm{rank}(A^*A)$, where $A^*$ is the conjugate transpose of $A$; this turns into the stated equality for real numbers.

Arturo Magidin
  • 417,286
  • 4
    More simply for $\operatorname{rank}(AB)\le\operatorname{rank}(B)$: take a basis $(v_1,\dots,v_r)$ of the range of $B,$ and notice that $A(v_1),\dots,A(v_r)$ span the range of $AB.$ – Anne Bauval Oct 05 '23 at 21:28
  • @AnneBauval, thank you! – user237522 Oct 05 '23 at 21:29
  • 2
    @AnneBauval I used the nullspaces because of the post linked at the end, which seeks a proof of $\mathrm{rank}(AB) = \mathrm{rank}(B)-\dim(\mathbf{N}(A)\cap\mathbf{R}(B))$, but sure. – Arturo Magidin Oct 05 '23 at 21:31
  • @ArturoMagidin, thank you for your proof. – user237522 Oct 05 '23 at 21:55
  • @user237522 who said it did? That comment has nothing to do with my answer, so why are you making it here? – Arturo Magidin Oct 07 '23 at 17:36
  • @ArturoMagidin, I apologize. I now deleted it. Just wanted to give an example over a field different from $\mathbb{R}$ or $\mathbb{C}$. – user237522 Oct 07 '23 at 18:35
  • @user237522 The result for $\mathbb{R}$ and for $\mathbb{C}$ rely on the fact that the transpose/conjugate transpose is the adjoint linear transformation relative to the standard inner product in each case. Fields of positive characteristic do not have positive definite inner products, so the notion of adjoint does not exist. – Arturo Magidin Oct 07 '23 at 19:43
  • @ArturoMagidin, thank you for the explanation. – user237522 Oct 07 '23 at 20:39
2

It is not necessary to use the rank-nullity theorem here. $\text{rank}(AB) \le \text{min}(\text{rank}(A), \text{rank}(B))$ not only holds over any field of any characteristic, it holds even if $A, B$ are linear operators on infinite-dimensional vector spaces, and the ranks can be infinite.

Here is the abstract argument. Let $U, V, W$ be three vector spaces and $B : U \to V, A : V \to W$ be two linear operators. Now:

  1. $\text{im}(AB)$ is a subspace of $\text{im}(A)$, so $\text{rank}(AB) \le \text{rank}(A)$.
  2. $\text{im}(AB)$ is the image of $\text{im}(B)$ under $A$ so it is a quotient space of $\text{im}(B)$, so $\text{rank}(AB) \le \text{rank}(B)$.

(In the infinite rank case we need the axiom of choice, I guess.)

Qiaochu Yuan
  • 468,795