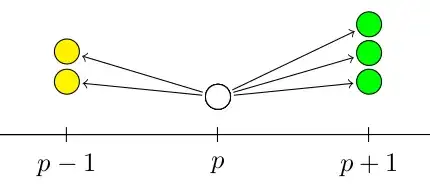
Consider the following simple branching random walk on $\mathbb Z$ in discrete time:
At stage 0, we start with one token at the site 0. At each time step, we randomly, independently split each token into either 2 tokens to the left, or 3 tokens to the right with probabilities $\frac35$, $\frac25$ respectively.
(I.e., a given token at site $p$ will split, uniformly randomly into either $2$ tokens on the site $p-1$, or $3$ tokens on the site $p+1$.)
Denote the number of tokens at site $p$ at the $n$th stage by $X_n(p)$, and denote the total number of tokens by $|X_n|$.
Question:
Does the observed distribution of tokens at the $n$th stage,
$$\mu_n = \frac1{|X_n|} \sum_{p \in \mathbb Z} X_n(p) \delta_{p},$$
almost-surely converge to a Gaussian distribution? (After a suitable rescaling.)
My numerical play suggests that it does, but I'm at a loss as to how to show it.