0

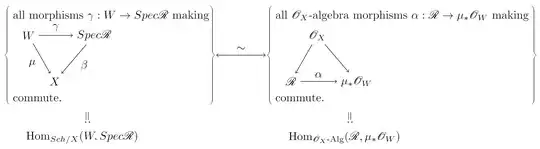
Given a scheme $X$ and a quasicoherent sheaf of algebras $\mathscr{R}$ on it. Vakil's FOAG, section 17.1.2, page 470 says that the relative spec $\beta: Spec \mathscr{R} \to X$, representing the following functor

$$ (\mu: W \to X) \mapsto \{(\alpha: \mathscr{R} \to \mu_* \mathscr{O}_W)\} $$

, i.e., there is a natural isomorphism between the following two sets

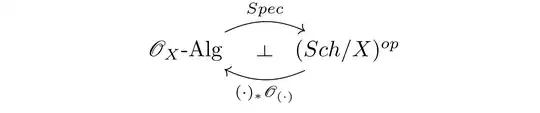
enter image description here

Does it imply that $Spec$ is left ajoint functor to the functor $(\cdot)_*\mathscr{O}_{(\cdot)}: (Sch/X)^{Op} \to \mathscr{O}_X\text{-Alg}$ that taking $\mu: W \to X$ to $\mu_* \mathscr{O}_W$?

enter image description here

Neither Vakil nor Stacks#01LQ says it's a left adjoint functor explicitly. However, Vakil mentions that $\mu_* \mathscr{O}_W$ maybe not quasicoherent (as in When is the pushforward of a quasi-coherent sheaf quasi-coherent? Hartshorne proof too). Being quasicoherent seems to be indispensable in the definition of the relative spectrum. Is this the reason for not being a left adjoint? Or is it a left adjoint?

Thank you in advance!

onRiv
  • 1,372

1 Answers1

1

As you suspected, $\operatorname{Spec}$ cannot be left adjoint to $(\cdot)_*\mathscr{O}_{(\cdot)}: (Sch/X)^{op} \to \mathscr{O}_X\text{-Alg}$, because it's not defined on sheaves of algebras that are not quasicoherent.

However, there's a adjunction in this situation. We have on the one hand the relative Spec functor from quasicoherent $\mathscr O_X$-algebras to schemes over $X$ and on the other hand, we can take a scheme over $X$ given by $\mu:W \to X$ and "quasicoherentify" $\mu_*\mathcal O_W$.

Compare this answer for some details on how to do this. It answers a related adjunction question.

Lukas Heger
  • 25,763