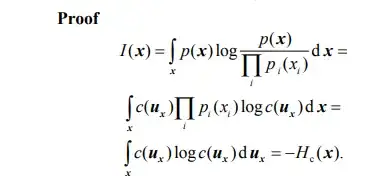I am trying to understand the proof of this paper (page 2). I don't understand how
the term $d \textbf{u} $ comes about. I get that $c(\textbf{u}_x) = \frac{p(\textbf{x})}{\prod_i p_i(x_i)}$ but don't know how it changes from $d\textbf{x}$ to $d\textbf{u}_x$.
Can someone show me the derivation please ?I am trying to understand the math.
The second to last equality is just an application of the change of variables formula. The original integral is performed with respect to ${\bf x}:= (x_1,x_2,\ldots,x_N)$ and we wish to change variables from $\bf x$ to ${\bf u}:=(u_1,\ldots,u_N)$ via the mapping $$u_1:=F_1(x_1),\quad u_2:=F_2(x_2),\quad\ldots,\quad u_N:= F_N(x_N).\tag1$$ By the change of variables formula, we can write $$\int h({\bf x})\,d{\bf x}=\int h({\bf x}({\bf u})){\left|{\det \left(\frac{\partial {\bf x}}{\partial{\bf u}}\right)}\right|}\,d{\bf u} = \int \frac{h({\bf x}({\bf u}))}{\left|{\det \left(\frac{\partial {\bf u}}{\partial{\bf x}}\right)}\right|}\,d{\bf u}.$$ For the mapping (1) the Jacobian determinant is easily seen to be $$\left|{\det \left(\frac{\partial {\bf u}}{\partial{\bf x}}\right)}\right|=\prod_{i=1}^N p_i(x_i), $$ which immediately yields the desired equality.
