23

I like math but I also like movies. I have been collecting movies all my life. My collection is rather huge: almost 25.000 movies. Being also a developer I was able to create my own online catalogue and pull various statistics from the database. There is one thing that puzzles me.

Movies have ratings and I did not invent mine: I have copied them from IMDb. As you probably already know, IMDb ratings go from 1 to 10, with 1 being the lowest. I have created a histogram representing ratings distribution and it looks like this:

IMDb movie ratings distribution

I expected to see something like normal distribution, but my histogram has a funny dip around rating 7.0.
Is this a known phenomenon in statistics?
Has anyone seen something like this in other data?

Prem
  • 14,696
Oldboy
  • 17,264
  • 2
    That is certainly interesting. I like data-mining myself. The value r = 7 is smack-middle if you started at r=4.8 (disregarding outliers) and ended at r = 9.2. Here is a related question from 2020 with informative comments but unfortunately no answer. – Tito Piezas III Jun 27 '23 at 07:38
  • 1
    We always found the same M-shaped distribution in the points given to math and thoretical physics exercises in those times of no access to information in the 1960-90 for students. All ratings define a dynamic process, separating the highly talented people from the rest. Both ensembles follow a gamma distribution for a Bessel process, but not for individuals, but for cohortes passing (many not ) the education process. – Roland F Jun 27 '23 at 08:34
  • 3
    Just to be clear, I take it the histogram is showing frequencies for the 25,000 films in your collection, is that right? (I'm judging roughly from the chart, but apparently IMDB has around 630k feature films). It would be interesting to see how the distribution looks for all films for comparison. – Chris Lewis Jun 27 '23 at 08:46
  • @ChrisLewis Yes, my movie database has approximately 25.000 rated titles in total. Unfortunately, I don't have data for all titles found on IMDb (only data for movies that I actually have in my collection) – Oldboy Jun 27 '23 at 10:27
  • 3
    I'd suggest another factor may be a discrepancy between ratings from critics and from audiences. As a film enthusiast you probably have quite a number of films in your list that are highly rated by critics but not so popular with a general audience. That sort of sampling could result in the type of bimodal distribution you're seeing. – Chris Lewis Jun 27 '23 at 12:34
  • @ChrisLewis I guess that in that case the number of critics would have to be roughly equal to (or at least comparable with) the number of ordinary viewers. In reality, I think that the number of critics is too small to produce bimodal distribution. – Oldboy Jun 27 '23 at 13:04
  • Critics and "ordinary viewers" who rate on IMDB. It's hard to be sure. The good news is the full dataset is available for free! (See my answer for a link.) – Chris Lewis Jun 27 '23 at 15:30

4 Answers4

16

You can get the full IMDB dataset (updated daily) from here !

On it (as of 27/06/2023) are 293,501 rated films. The distribution of their rating is shown below:

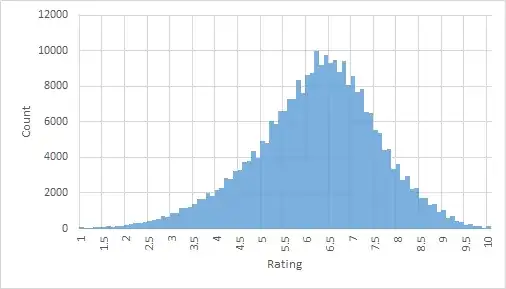
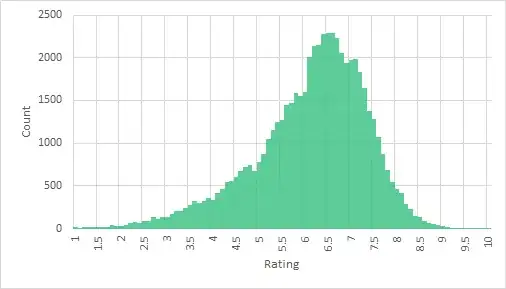
enter image description here

As you can see, the full dataset doesn't show the same bimodal distribution as the curated sample in the question.

This suggests that the sampling is producing this bimodality. There are lots of possible reasons for this but perhaps the datasets will let you explore a bit more.

Many of the films have 500 votes or fewer. If we discount those, we're left with around 58k films whose ratings distribution is below:

enter image description here

One striking fact about these charts is quite how high the ratings are. It seems a rating of 5 does not correspond to an "average" film. Perhaps you get a few ratings points for making a film at all ;-).

Chris Lewis
  • 3,641
  • 1
  • 6
  • 11
  • 5
    Or the ratings are biased in that the ones on the really bad end of the scale have mostly just faded into well-deserved obscurity and are not seen and rated by enough people to register? I've seen some listings on there that you'd have to personally know the filmmaker in order to get a copy of it. Many older and lesser-known titles may not even have any surviving copies anymore, but they're still listed. – Darrel Hoffman Jun 27 '23 at 16:03
  • 1
    I've always felt that many people rate films on an American grade distribution, where below 70 is considered failing. – Brady Gilg Jun 27 '23 at 17:23
  • 1
    I have generally seen "movie raters" Indicate Average movie with 6-7 rating , Best movie with rating 9-10 & Bad movie with rating 4-5 , @BradyGilg , Horrible movie gets 2-3 rating , while 1 rating is reserved for review-bombing Cases. Partially , that may Explain the Bias here ! – Prem Jun 27 '23 at 17:42
  • 2
    @DarrelHoffman, it's a well-known phenomenon that nobody ever uses the lower half of a ten-point rating scale. (And on a five-point scale, nobody ever rates something a "2".) – Mark Jun 28 '23 at 01:35
  • 3
    It was always the running joke in our family that every movie has a 6.7 rating on IMDB. Didn't matter how good or bad it was, it'd be around there. Nice to see this wasn't just our imagination. – Luke Sawczak Jun 28 '23 at 03:35
  • One would hope that a good movie (i.e. one that people like) would have a greater chance of getting through financing and filming and release and whatnot (that a lot of people may need to sign off on) than a bad movie. Plenty of bad movies still get made, sure, but it makes sense that the ratings would skew positive. – NotThatGuy Jun 28 '23 at 13:50
  • @NotThatGuy But all movies would be rated against the ones that have been made, not the ones that didn't get produced. Another thing that might be interesting is to look at distributions of votes for individual films. I can't imagine there are many, say, pure 7s out there (where everyone agrees, yes, this film is 7/10). My guess would be that people motivated enough to vote would tend to vote high ("best film ever!") or low ("why did this get such a good rating?! I must correct it!), but perhaps that's not the case among people with IMDb accounts. Unfortunately that isn't in the IMDb dataset – Chris Lewis Jun 28 '23 at 14:02
  • There are multiple causes for bias: Moviegoers aren't going in blindly, they choose movies that they expect to like, and they're usually right. Movie studios try to avoid making bad movies; they don't always succeed, but most movies that get to theatres are decent. Ratings are on an absolute scale, not relative to the universe of movies that get to theatres; so 0 is the worst possible movie, not the worst available movie, and no one makes those. – Barmar Jun 28 '23 at 16:10
6

This is known as a "bimodal distribution". The modes is this case are close together, so it's not a very strong effect. You could model the distribution as being the sum of two normal distributions with slightly different means; i.e., there are two "types" of movies that you like, one that averages slightly higher ratings than the other.

The idea that distributions tend to be normal comes from the fact that a lost of numbers come from a bunch of different effects, each one only a small percentage of the total effect, and uncorrelated or not very correlated with the others. Bimodality suggests that there are some factors that have very large effect, and/or are strongly correlated with each other. It could be that there's two clusters of movies, one slightly better than the other. Or there's one cluster of reviewers that tend to give slightly below 7, and another slightly above, and they tend to review different movies. But given that according to Chris Lewis' charts, movies in general are not bimodal, it seems that there are two clusters of movies that you've collected. For example, maybe half of your movie collection was chosen by you, and the other half was chosen by your partner.

Bimodality is one characteristic than can distinguish a distribution from a normal one. Other ones are what are called "higher moments". The first moment describes where the center is, and the second describes how spread out it is. These two moments vary from one normal distribution to another, and knowing these two moments and that a distribution is normal tells you what its value everywhere is. For a normal distribution, all moments past the second are determined by the first two, so if the actual moments don't match what they would be for a normal distribution, that's another way the distribution deviates from normality.

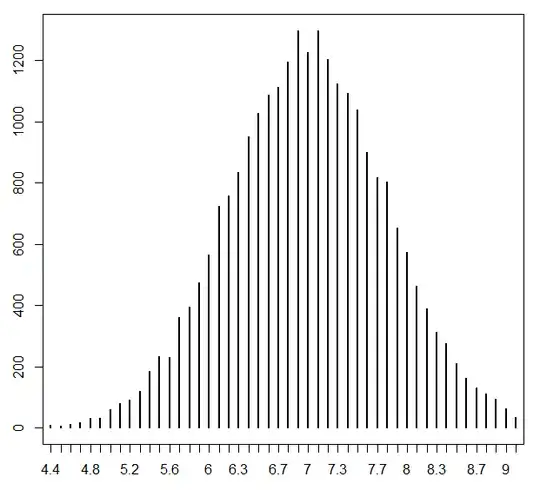
The third moment basically measures how symmetrical the distribution, and corresponds to "skew". A normal distribution is perfectly symmetrical, and thus has zero skewness. Your distribution has negative skew, which means that it fades away more slowly on the right than it does on the left.

Acccumulation
  • 12,864
3

It is a case of a Bimodal Distribution which will have two Peaks.

In general , these Bimodal Distributions are a "mixtures" of 2 Unimodal Distributions , which may be hidden.

Here , I would guess (because I do not have more Details to figure out) that the IMDB users are of 2 general types : "those who think average movies should have average rating which is ~6" & "those who think average movies should have average rating which is ~7". Put the users together & we will get 2 Mode values with 2 Peaks.

When we are able to group the users into those 2 types & then make the Individual Charts , we will get 2 Unimodal Distributions.

Intuitive Examples:

(1) When we make the Distribution of Weight/Height/Speed-to-run-100-meters/Strength-to-lift/Etc among Population in general or among Olympic Players , we may get Bimodal Distribution.

When we make the Distribution of Weight/Height/Speed-to-run-100-meters/Strength-to-lift/Etc among male Population or among male Olympic Players , we may get Unimodal Distribution.
Likewise , we will Unimodal Distribution among females.

The merger will give Bimodal Distribution.

(2) There are Cases with more than 2 Peaks , Multimodal Distributions , which are "mixtures" of more than 2 Unimodal Distributions.
Distribution for "Time of Maximum-Customers" in Canteens may have 3 (or 4) Peaks during breakfast , lunch (& evening tea time) & Dinner.

Prem
  • 14,696
  • Why would raters fall into those discrete categories, rather than their thoughts on "average ratings" (or, more realistically, their personal average ratings) themselves being continuously distributed? – Sneftel Jun 28 '23 at 10:41
  • In School & College , I have come across teachers & lecturers whose Evaluation Standards are known : "Oh , I will avoid teacher A , who will always fail 10% of the class" & "Oh , I am taking the Course by teacher B who never gives failing grades" : Naturally , when we group those teachers , we will get Bimodal grades. Likewise , movie audiences may (I have no knowledge in general or even county-wise or age-wise) have tendencies to unconsciously form various "average" rating groups. Movie Industry Insiders may have Details on this , @Sneftel , I have no access. I can not do more than guess. – Prem Jun 28 '23 at 11:00
  • I don't know of many IMDB users who have formal, quantitatively specified "evaluation standards". It just seems like an awfully artificial interpretation of a single histogram, given the wealth of other possibilities raised by other answers. – Sneftel Jun 28 '23 at 11:55
  • (1) I too have no formal Standards , hence I specifically said "tendencies to unconsciously form various" (2) About "the wealth of other possibilities" , mine was the first Answer here , there was no other Answer at that time. (3) I too do not know many IMDB users , @Sneftel , hence , other than guessing , I can not generalize on what they might think. (4) I think your Same Objection can be made to the other Answers : Why claim noise when other Answers are Possible ? Why claim Single Peak when other Answers are Possible ? (5) Even though my Answer is not Accepted , it might be true !! – Prem Jun 28 '23 at 12:11
2

That may just be noise.

Your distribution does not really have a normal distribution (the plateaued peak from about $6.4$ to $7.4$ is wide compared to how fast the distribution falls away either side of this, particularly on the left) but, even if it did, you could easily see something similar.

Here is a simulated example using R with $25000$ samples from a normal distribution and it also has a dip about $7.0$. Using a different seed would give a different pattern of peaks and troughs in the middle of the distribution but similar noise.

set.seed(2023)
plot(table(round(rnorm(25000, 7, 0.8), 1)), xlim=c(4.5, 9.0))

enter image description here

Henry
  • 169,616
  • 2
    I am not sure it is noise. In your Chart , we see the "Single Dip" , which may be noise. In OP Chart , it is clearly going down & then shooting back "Between 2 Peaks" , which is a large range & unlikely to be "Co-Ordinated" noise ! – Prem Jun 27 '23 at 10:33
  • 1
    @Prem Try plot(table(round(runif(25000, 5.95, 8.05), 1))) with different seeds. Some of them will have places where it clearly goes down and then shoots back up even though the sampling is from a uniform distribution. You cannot prove it is noise, but you have to consider the possibility. – Henry Jun 27 '23 at 10:57
  • I agree that we have to consider that Possibility & your Post indicates that , though it may be better to Explicitly State that it is the Alternate Interpretation. People like me may tend to miss out the May in your Initial line !! – Prem Jun 27 '23 at 11:13
  • 2
    The peak is around 1300, square root of that is about 36. The chart goes down twice in each direction, each time by around 100. If we take the very rough approximation of std = sqrt(expected value), that's three standard deviations. It's easy to believe in getting 3 std by chance once, but getting it three times is highly unlikely. – Acccumulation Jun 28 '23 at 01:08
  • @Acccumulation Maybe. Or perhaps the changes are rather smaller than 100, and you have nine or ten values all very similar with some random ordering of the noise which natural human instinct is to try to spot a pattern. You would not test this with Chris Lewis's blue chart for the whole distribution but you might instead test a parity pattern on the first decimal place, but perhaps skewness on the green chart. There are a lot of potential patterns in exploratory data analysis. – Henry Jun 28 '23 at 07:59