0

Question: Suppose we have a curve $$\mathcal{S} :\ ax^2+by^2+2hxy+2gx+2fy+c=0$$ and a straight line $$\mathcal{L} :\ lx+my+n=0$$ where $n \ne 0$ and we have the homogenized curve of them $$\mathcal{S}' :\ ax^2+by^2+2hxy+2(gx+fy)\left(\frac{lx+my}{-n} \right)+c\left(\frac{lx+my}{-n}\right)^2=0$$ then prove or disprove the following statement : "If $\mathcal{L}$ intersects $\mathcal{S}$ at exactly one real point then $\mathcal{S}'$ represents a pair of real coincident lines passing through origin and through the point of intersection of $\mathcal{S}$ and $\mathcal{L}$."

What this statement basically concludes is that by the very definition of homogenization all the lines of $\mathcal{S'}$ must represent the line passing through origin and point of intersection of $\mathcal{S}$ and $\mathcal{L}$ but that clearly fails as in the example taken below.

My Attempt: Now I could not formally prove anything in this but I was able to find a counterexample of this which does disprove this but I don't know the logic behind this so any explanation would be helpful, here's the example :

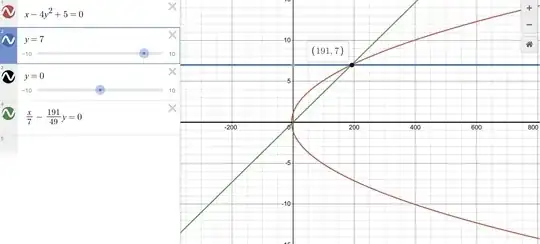
Let $$\mathcal{S} :\ x - 4y^2 +5 =0$$ $$\mathcal{L}:\ y=7 $$ then $$\mathcal{S}' :\ x\left(\frac{y}{7}\right)-4y^2 +5\left(\frac{y}{7}\right)^2 =0 \implies y\left(\frac{x}{7}-\frac{191}{49}y \right)=0$$ Clearly $\mathcal{S}'$ does not represent a pair of coincident lines.

enter image description here

Why is the line $y=0$ coming?

lilychou
  • 1,475
  • Why clearly? $y\left(\frac{x}{7}-\frac{191}{49}y \right)=0$ are the two lines $y=0$ and $y=\frac{7}{191}x$; they meet, so I'd say they are coincident. And $y=\frac{7}{191}x$ does go through the intersection point $(191,7)$ of $x - 4y^2 +5 =0$ and $y=7.$ – Jan-Magnus Økland Jun 18 '23 at 18:11
  • @Jan-MagnusØkland I think you got the wrong idea. What I mean by coincident is that those two lines must be the same line or in other words for a non zero $\lambda$, $\mathcal{L_1}=\lambda \mathcal{L_2}$. – lilychou Jun 18 '23 at 18:23
  • See this. – Jan-Magnus Økland Jun 18 '23 at 18:25
  • Please format non-mathematical text using markdown, for instance **bold** for bold. I've made the change for you in this post this time. – KReiser Jun 18 '23 at 18:30
  • Hint: Thinking projectively, what is the other intersection point? (For the lines to coincide you'd need a tangent.) – Jan-Magnus Økland Jun 18 '23 at 18:59

1 Answers1

1

The projective situation is $\langle xz-4y^2-5z^2,y-7z\rangle$ which is $\langle x-191z,y-7z\rangle$ and $\langle y,z\rangle.$ This means that the line intersects the parabola also at the line at infinity along the $x$-axis or $y=0.$

Jan-Magnus Økland
  • 6,019
  • can you elaborate a little more on how to take a projection per se – lilychou Jun 19 '23 at 08:42
  • @sparrow_2764 The projection is what you started with and you can get back by setting $z=1.$ The unprojection or homogenization are the cones over the equations. In this case it's an actual cone and a plane, that intersects in two lines that project to two points. – Jan-Magnus Økland Jun 19 '23 at 09:45