1

Borrowing from Ohn (1999)1 and shortening the notation, it seems that a convex shape on a hexagonal grid can be produced by proceeding in the first of six directions an integer distance $e_0$, turning right by 60° and proceeding a distance $e_1$ and repeating to produce the six-tuple $e_0, e_1, e_2, e_3, e_4, e_5$ such that you return to the starting position.

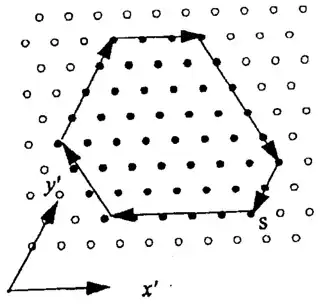
Figure 3. Example HCSE (hexagonal convex structuring element) P. The chain code of the boundary of P is 051324334552 starting with point S. click for full size

Figure 3. Example HCSE (hexagonal convex structuring element) P. The chain code of the boundary of P is 051324334552 starting with point $S$.

If as shown in the image below ($e_0, e_1, e_2, e_3, e_4, e_5 = 5, 3, 4, 3, 5, 2$) the directions $\hat{x}$ and $\hat{y}$ form an acute 60° angle with $e_3$ counted in the $\hat{x}$ direction and $e_2$ counted in the $\hat{y}$ direction, and assuming we start at position (0, 0), the final position will be given by.

$$x=-e_0 - e_1 + e_3 + e_4$$ $$y=e_1 + e_2 - e_4 - e_5$$

If I want to generate all convex shapes with maximum side length $n_{max}$ (counting all six rotations of a given shape as distinct), I can first generate all six-tuples with $0 \le e_i \le n_{max}$ then keep only those that represent closed paths, i.e. that satisfy

$$e_0 + e_1 = e_3 + e_4$$ $$e_1 + e_2 = e_4 + e_5$$

If I don't want to consider the sixfold rotations of a shape as distinct, I (think that I) can discard any six-tuple that is a cyclic permutation of a previous six-tuple.

I can imagine how to reconstruct all of the lattice points on the perimeter2, but I don't know how to find all of the lattice points inside as well.

Question: Find all points in a closed convex shape drawn on a hexagonal lattice using chain codes (lengths of sides)

In other words, I want to plot all the filled circles (occupied lattice points) shown in the image, not just the $n = e_0 + e_1 + e_2 + e_3 + e_4 + e_5$ points on the edge.

1Syng-Yup Ohn (1999) Optimal Decomposition of Convex Structuring Elements on a Hexagonal Grid The Jourmal of the Acoustical Society of Korea, Vol. 18. No. 3E

2For the example these would be $(0, 0), (-1, 0), (-2, 0), (-3, 0), (-4, 0), (-5, 0), (-6, 1), (-7, 2)... (-2, 4), (-1, 3), (0, 2), (0, 1)$

uhoh
  • 1,967

1 Answers1

1

This is more a collection of hints than a fully-worked out answer, but here goes:

You can easily get the number of points on the boundary, and you can get the area enclosed as an integral around the boundary. Then you need a version of Pick's Theorem that holds for the hexagonal lattice to get an equation relating the number of boundary points, the area, and the number of internal points. The discussion at Pick's Theorem on a triangular (or hex) grid says there isn't any such version of Pick's Theorem, but there is an approximate version that may be good enough for your purposes.

Gerry Myerson
  • 185,413
  • Thanks I will take a look. I just left a comment under the question about "space filling curve based on the Gosper fractal" which might (or might not) work here as well. – uhoh Jun 16 '23 at 11:36
  • The number of interior points can easily be worked out by completing to the large equilateral triangle and subtracting accordingly. $\quad$ In the general case for the hexagonal board, there is no formula that depends only on those variables. – Calvin Lin Jun 16 '23 at 11:36
  • @CalvinLin ya I just need an algorithm for finding each of interior points, not a formula for the number of them. – uhoh Jun 16 '23 at 11:38
  • I think the idea of @Calvin can work for finding the points, not just the number of points. Complete to a large equilateral triangle; it should be easy to list all the points in that triangle, and to list the points in the three small triangles that are outside the hexagon, and delete the second set of points from the first. – Gerry Myerson Jun 16 '23 at 11:55
  • @GerryMyerson okay the convex shapes can be anything from a single row (0n00n0), to an equilateral triangle (0n0n0n), to irregular quads, pents or hexes. I wouldn't know how to begin to "complete to a large equilateral triangle" for such a variety of shapes much less know what to do next. While I'm faced with this challenge today, it's a whole new thing for me. Hopefully algorithmicly-minded individual will have mercy on me and find spelling out the procedure worthwhile :-) – uhoh Jun 16 '23 at 12:09
  • 2
    If there aren't any zeros, then you're guaranteed to get a hexagon, aren't you? Now if you get a hexagon, like the one in your picture, you can extend the 2nd, 4th, and 6th sides until they intersect each other, and that gives you a big equilateral triangle, which consists of your hexagon plus a smaller equilateral triangle at each corner. I expect that in your quad and pent cases, similar extensions of sides will result in big equilateral triangles formed by the quad or pent and one or more small equilateral triangles. – Gerry Myerson Jun 16 '23 at 12:53
  • @GerryMyerson Okay, yes I get the idea now. :-) I'll take a look in the morning, thanks! – uhoh Jun 16 '23 at 13:59
  • ...but I think that's going to be fairly messy algorithm to write such that it covers all edge cases; I wish there was something that didn't involve constructions. – uhoh Jun 16 '23 at 14:48
  • 1
    @uhoh It's a very simple approach, very little mess from what I can tell. If you get stuck, show what you've tried and ping me to help you work it out. – Calvin Lin Jun 16 '23 at 16:11
  • 1
    I got stuck... dealing with other deadlines, not mathematically. I really want to accept this as I now see how this is going to work even though I haven't come back to implement it... yet. If I wait another month I may forget, so here goes! Thanks! – uhoh Aug 09 '23 at 21:10