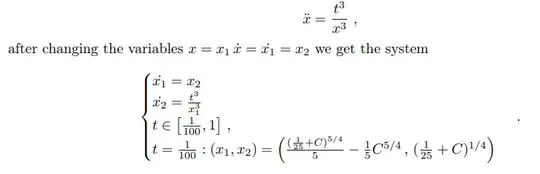0

Here is what I tried to do enter image description here

But it was a long time since I took ODE course, so I might be doing something wrong. I need to get it to some form of vector system of first order which would look like $$\frac{dX}{dt} = F(t, X(t))$$ for applying Runge-Kutta algorithms, like it described in this question for example: $2$-dimensional Runge-Kutta for system of polynomial ODEs

Could you please give me advise on how can I do it properly?

I don't know if my guess is right, but I feel like instead I should look for a change of this form $$t = e^{\tau} \, , \, x = ze^{2\tau} \, ,$$ where $z = z(\tau)$ is the new function.

To be fair, the first case doesn't look like a valid change at all.

Petya Balabanov
  • 386
  • 1
    Writing $y=1/x$, the differential equation appears to become $\ddot{y}=\dot{y}^2-t^3 y^3$. Hence $d/dt(y,\dot{y})=(\dot{y},\dot{y}^2-t^3 y^3)$ which appears to be of the desired form. – Semiclassical Jun 01 '23 at 17:17
  • See this https://math.stackexchange.com/questions/2615672/solve-fourth-order-ode-using-fourth-order-runge-kutta-method – Vasili Jun 01 '23 at 17:24
  • $$X=(x_1,x_2)$$ $$F(u,v)=F(u,v_1,v_2)=\left(v_2,;\frac{u^3}{v_1^3}\right)$$ $$\frac{dX}{dt}=F(t,X)$$ – mr_e_man Jun 01 '23 at 17:35
  • @Semiclassical could you clarify how did get this equation? I tried this and I got $\frac{\ddot{y}}{y^2} = \frac{2\dot{y}^2}{y^3} - y^3t^3$ – Petya Balabanov Jun 01 '23 at 18:14
  • @Vasili they only look at the case of linear ode there, in my case I don't know what to do with $\ddot{x}x^3 = t$ – Petya Balabanov Jun 01 '23 at 18:36
  • You're right that my derivation was goofy. I do seem to get $y^4 t^3$ in the third term rather than $y^3 t^3$, but this could be a typo on my part. – Semiclassical Jun 01 '23 at 19:14
  • @Semiclassical But what's the point of $y = \frac{1}{x}$? Why $\frac{d}{dt}(x, \dot{x}) = (\dot{x}, \frac{t^3}{x^3})$ is not good enough? My teacher said that it doesn't lower equation's order, but I don't see why – Petya Balabanov Jun 01 '23 at 19:33
  • 2
    @PetyaBalabanov - It is good enough. Maybe Semiclassical thought you wanted a polynomial system. -- You asked how to write it as a first-order vector equation. It is $$\frac{d}{dt}(x_1,x_2)=\left(x_2,;\frac{t^3}{x_1^3}\right).$$ Are you still missing something? – mr_e_man Jun 01 '23 at 19:41

0 Answers0