1

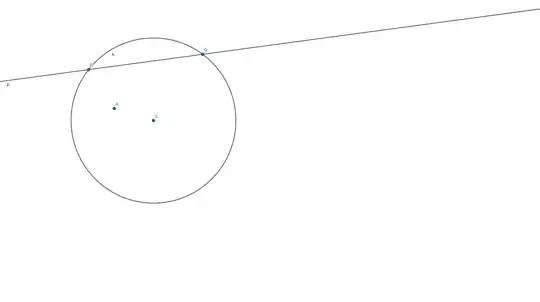
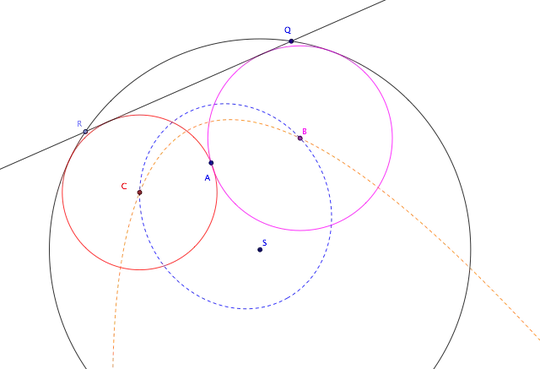
Circle k and a line p that intersect at points R and Q are given. Inside the circle point A is given. Construct all the circles that touch the line p and the circle k and pass through the point A.

I tried to solve this problem using homothety, but it didn't work out so I guess that's not the proper way to solve it. I would appreciate any ideas.

enter image description here

Katarina
  • 429
  • 1
    See here: https://www.cut-the-knot.org/Curriculum/Geometry/GeoGebra/PLC.shtml – Intelligenti pauca May 17 '23 at 16:31
  • 1
    Do you know about inversion? If so, then inversion about $R$ for example will transform the problem into a simpler one (and in fact that other problem can be solved using homothety). – Daniel Schepler May 17 '23 at 16:58
  • @DanielSchepler If I understoond you correctly, the idea is to find the inverse image of the original circle with respect to some arbitrary circle centered at R? And the image of the original circle will be a line so the problem is now reduced to finding a circle that touches the original line, the line obtained by inversion and passes through the point A? – Katarina May 18 '23 at 09:59
  • @DanielSchepler So I did find the inverse image of the given circle with respect to the circle centered at R ( I chose two different points on the original circle and found their inverse images with respect to the circle centered at R). So now I have two lines, and the given point A. Then I applied homothety to find a circle that passes through A and touches both lines, but the obtained circle doesn't touch the original circle as its requested. I probably misunderstood your hint – Katarina May 18 '23 at 11:41
  • 1
    The idea is indeed to perform inversion about some circle centered at $R$; use a homothety to find circles tangent to two lines (the line $p$ and the image of the circle $k$) and through the image of $A$; and then perform inversion again about the circle centered at $R$. That will give you the circles tangent to $p$ and $k$ and passing through $A$. – Daniel Schepler May 18 '23 at 15:20

1 Answers1

1

The centers of those circles are the intersections between an ellipse and a parabola. See figure below.

enter image description here

Intelligenti pauca
  • 55,765