1

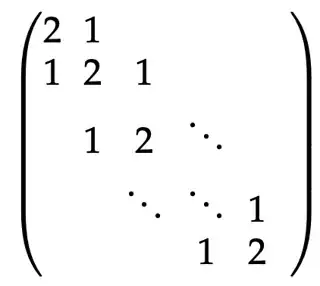
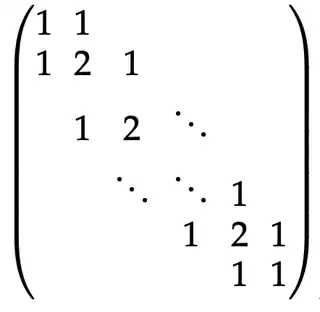
I am trying to find the eigenvalues of the following two $n \times n$ symmetric tri-diagonal Toeplitz matrices (let us call them $A$ and $B$ respectively):

enter image description here

enter image description here

Note that the standard way of computing the eigenvalues is by computing the characteristic polynomial and then finding the roots of the same. This seems to be done in this paper, in Lemma $43$ --- moreover the characteristic polynomial of one of these matrices seems to be a function of the characteristic equation of another --- but the steps are not clear.

RandomMatrices
  • 387
  • 1
    None of them is a block diagonal matrix. They are symmetric tridiagonal matrices. – user1551 Apr 11 '23 at 10:00
  • Sorry! Made the edit. – RandomMatrices Apr 11 '23 at 13:42
  • 1
    Hi, you should be even more specific as these matrices are triagonal Toeplitz matrices (constant diagonals). There are numerous examples on the internet (even on the wikipedia page) for this very particular case. – Lelouch Apr 11 '23 at 13:43
  • Updated the question again. The first matrix is indeed a tridiagonal Toeplitz matrix. How about the second matrix though? I am using this answer (https://math.stackexchange.com/questions/955168/how-to-find-the-eigenvalues-of-tridiagonal-toeplitz-matrix) as a reference, which has the same constant entries in all the diagonals. This is not true for the second matrix. @Lelouch – RandomMatrices Apr 11 '23 at 14:25
  • Your second matrix is not a Toeplitz matrix (unless $\ n=2\ $) because the entries along its main diagonal are not constant. The entries in row $1$, column $1$ and row $\ n\ $, column $\ n\ $ are both $1$, whereas the entries in row $\ j\ $, column $\ j\ $ are $2$ for all other $\ j\ne1,n\ $. – lonza leggiera Oct 09 '23 at 08:00

3 Answers3

1

Consider the first matrix $A$ of dimension $n\times n.$ It suffices to determine the eigenevalues of $C=A-2I.$ Let $v_t=\left \{{\sin kt\over \sin t }\right \}_{k=1}^n $ for $0<t<\pi.$ Then $v_t\neq 0$ as the first coordinate is equal $1.$ We have $$(Cv_t)_k= \begin{cases} \displaystyle {\sin (2t)\over \sin t} & k=1\\ \displaystyle{\sin (k-1)t\over \sin t }+{\sin (k+1)t\over \sin t } & 2\le k\le n-1\\ \displaystyle{\sin (n-1)t\over \sin t } & k=n \end{cases}\\ = \begin{cases} \displaystyle 2\cos t & k=1\\ \displaystyle 2\cos t {\sin(kt)\over \sin t} & 2\le k\le n-1\\ \displaystyle 2\cos t {\sin(nt)\over \sin t}-{\sin(n+1)t\over \sin t} & k=n \end{cases} $$ Let $t_m=\displaystyle {m\pi\over n+1},$ $1\le m\le n.$ Then $\sin(n+1)t_m=0$ and $$Cv_{t_m}=(2\cos t_m) v_{t_m},\quad 1\le m\le n$$ In this way we have obtained $n$ different eigenvalues $2\cos t_m$ of the matrix $C.$ Hence the numbers $2+2\cos t_m,$ $1\le m\le n,$ are the eigenvalues of $A.$

Ryszard Szwarc
  • 44,675
1

For matrix $B$ it seems to be $2-2\cos\frac{k\pi}{n}$ , $ 0 \leq k \leq n-1$, at least for small $n$ values.

Lelouch
  • 1,938
  • 4
  • 9
  • Might you explain why that is the case? Is there a more general formula for almost-Toeplitz matrices like matrix $B$? – RandomMatrices Apr 11 '23 at 17:01
  • I just computed for the first values of $n$. I dont think there is a general formula for non toeplitz tridiagonal matrix but for this special "almost toeplitz" case this ismaybe possible. Just apply the same method that with a toeplitz matrix using a system of differences equations. The only change will be with the boundary conditions (first and last equations). Maybe this can lead to an answer. – Lelouch Apr 11 '23 at 17:15
0

I am a bit late to the party but your B matrix is a perturbed 2-Toeplitz matrix, for which you can find analytical expressions for the characteristic polynomial (not sure you will be able to solve those analytically for your matrix). Check "The Characteristic Polynomial of Some Perturbed Tridiagonal k-Toeplitz Matrices" from Fonseca

lyapunov00
  • 3
  • As it’s currently written, your answer is unclear. Please [edit] to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers in the help center. – Community Oct 09 '23 at 07:47
  • A complete study of the eigenvalues of matrices essentially of the form $T+T^T+S(a,b)$ where $T$ is triangular Jordan and $S(a.b)$ is zero everywhere except in s_11=a and s_nn=b is in Applied Mathematics E-Notes, 5(2005), 66-74 c ISSN 1607-2510 Available free at mirror sites of http://www.math.nthu.edu.tw/∼amen/ EIGENVALUES OF SEVERAL TRIDIAGONAL MATRICES ∗ Wen-Chyuan Yueh – Gérard Letac Oct 09 '23 at 08:45
  • Indeed, the work from Yueh also adresses this topic, I personally prefer the approach based on Chebyshev polynomials – lyapunov00 Oct 09 '23 at 11:56