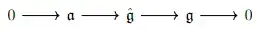3

I am currently reading Edward Frenkel's "Langlands Correspondence for Loop Groups", freely available here: https://math.berkeley.edu/~frenkel/loop.pdf.

In the appendix $A.4$ he describes central extensions of Lie algebras: let $\mathfrak{g}$ and $\mathfrak{a}$ be Lie algebras over the same field, with $\mathfrak{a}$ abelian. We say that $\hat{\mathfrak{g}}$ is an extension of $\mathfrak{g}$ by $\mathfrak{a}$ if there exists a short exact sequence of Lie algebras

enter image description here

We also require that $\mathfrak{a}$ is central in $\hat{\mathfrak{g}}$, that is $[a,x]=0$ for all $a\in \mathfrak{a}$ and $x \in \hat{\mathfrak{g}}$.

Now the part I don't understand, he says: suppose that $\mathfrak{a}$ is one dimensional, with generator $v$. As a vector space $\hat{\mathfrak{g}}$ is isomorphic to $\mathfrak{g}\oplus \mathbb{C}v$, and he declares that "the Lie bracket on $\hat{\mathfrak{g}}$ gives rise to a bracket on $\mathfrak{g}\oplus \mathbb{C}v$ such that $$[x,y]_{new}=[x,y]_{old}+c(x,y)v$$ where $x,y \in \mathfrak{g}$ and $c \colon \mathfrak{g}\otimes \mathfrak{g} \to \mathbb{C}$ is a linear map".

I can't see why the difference $[x,y]_{new}-[x,y]_{old}$ must lie in $\mathfrak{a}$, and thus be a multiple of $v$.

Can someone please enlighten me? This is not a homework question.

Thanks in advance

toyr99
  • 201
  • 1
    write elements of $\hat{\mathfrak{g}}$ as $(x + a)$ and expand the bracket $[x+a, y+b]_{new}$. Since $a$ and $b$ are central, two of the summands will vanish – Grisha Papayanov Mar 15 '23 at 15:49
  • I did that already, and $[x+a,y+b]=[x,y]$, but I can't see how this can help me. – toyr99 Mar 15 '23 at 15:50
  • 1
    The value of $[x, y]{new}$ is an element of $\mathfrak{g} \oplus \mathfrak{a}$, not of $\mathfrak{g}$. It has two components. The fact that the projection $\mathfrak{g} \oplus \mathfrak{a} \rightarrow \mathfrak{g}$ is a Lie algebra map tells you that the first component coincides with $[-,-]{old}$, but the second component may be nontrivial. – Grisha Papayanov Mar 15 '23 at 15:55
  • Thanks a lot, that's what I was missing. If you want to post an answer I'll gladly accept it – toyr99 Mar 15 '23 at 15:59
  • 1
    Glad to be of help – Grisha Papayanov Mar 15 '23 at 16:02

1 Answers1

2

The value of $[x,y]_{new}$ is an element of $\mathfrak{g}⊕\mathfrak{a}$, not of $\mathfrak{g}$. It has two components. The fact that the projection $\mathfrak{g}⊕\mathfrak{a}→\mathfrak{g}$ is a Lie algebra map tells you that the first component coincides with $[−,−]_{old}$, but the second component may be nontrivial.

Grisha Papayanov
  • 146