How to prove this theorem for the number of components of a filled julia sets?

Question

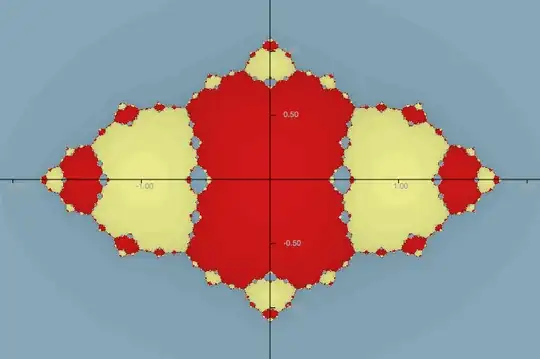
If one finite critical point of $f(z)$ escapes to infinity by iterating, then the filled-in Julia set of $f(z)$ consists of infinitely many components.

How to prove this ?

I must admit I heard this in the context of polynomials so maybe there are restrictions on $f(z)$ ?

Does $f(z)$ need to be a polynomial ? Or is entire sufficient ? Or does $f(z)$ need to be an entire and fast converging taylor series ? Maybe $f(z)$ needs to be bounded in some way like $|f(z)| < C \exp(|z|) $ or such.

So , my question is two-fold :

1. What is the exact most general definition of the theorem ?
2. How to prove this theorem or maybe theorems if we consider the stronger versions ?

Answer 1

Your statement is definitely true for polynomials, though not necessarily easy to prove. This is a consequence of theorem two theorems in Alan Beardon's Iteration of Rational Functions, namely:

Theorem 9.5.1 which states, in part, that the basin of attraction of $\infty$ is simply connected if and only if it contains no finite critical points

and

Corollary 7.5.5 which states that if a component of the Fatou set of a rational function contains a fixed point (such as $\infty for a polynomial), then that component is either simply connected or infinitely connected.

A simple example is $f(z) = z^2 - z^3/9$, which has a fixed critical point at $0$ and another critical point at $6$ that escapes to $\infty$.

---

For rational maps, it is not true that if one finite critical point of $f(z)$ escapes to infinity by iterating, then the filled-in Julia set of $f(z)$ consists of infinitely many components. A rational counter example is $$ R(z) = \frac{z^8-4 z^6+4 z^4}{2 z^4-4 z^2+1}. $$ Note that $R = f\circ f\circ f$, where $$ f(z) = \frac{1}{z^2-1}. $$ The function $f$ has exactly one super-attractive, periodic orbit namely $$0 \to -1 \to \infty \to 0.$$ Those points are all super attractive fixed points under iteration of $R$. An image of the basins of attraction look something like so: