Pseudo Euler's identity (continuous) $ \int_{0}^{\infty} \frac{\pi^x}{\Gamma (x+1)} e^{\frac{i \pi x}{2}} dx =?$

Question

Euler identity can be rewritten in a summation notation. Here I replaced the summation with an integral and Gamma function for factorial. According numerical analysis and WA (online) this integral seems to converge. Question: How to solve integral and were does this sort of continuous Euler's identity occur in math applications? Method: $e^{i\pi}+1=0$.

With (Taylor): $$e^{x}=\sum_{k=0}^{\infty} \frac{x^k}{k!}\text{ and }i^k= e^{(i \pi k)/2}$$

Euler (discrete): $$e^{i \pi}=\sum_{k=0}^{\infty} \frac{\pi^k}{k!} \left(\cos \left(\frac{\pi k}{2} \right) + i \sin \left(\frac{\pi k}{2} \right)\right) = -1$$

Then I took the freedom to rewrite it in a sort of continuous notation: (edit: from comment @eyeballfrog, gamma + 1. plot updated).

Pseudo Euler (continuous): $$ \int_{0}^{\infty} \frac{\pi^x}{\Gamma (x+1)} \left(\cos \left( \frac{\pi x}{2} \right) + i\sin \left(\frac{\pi x}{2}\right)\right) dx $$

$$ \int_{0}^{\infty} \frac{\pi^x}{\Gamma (x+1)} e^{\frac{i \pi x}{2}} dx =?$$

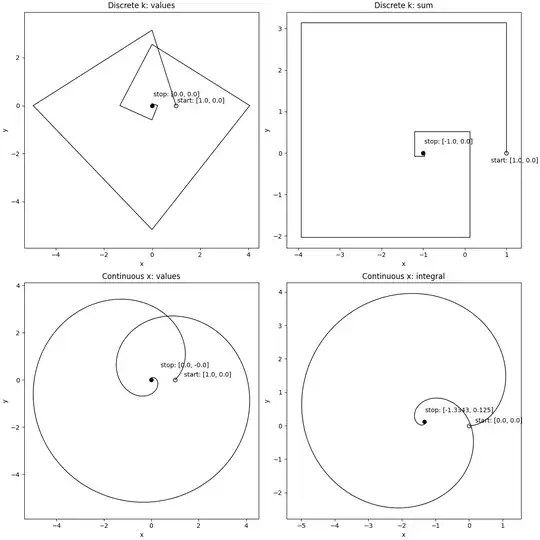
Did numerical analysis see plot below. This matched the answer given by WA (without method): $ \int_{0}^{\infty} \frac{\pi^x}{\Gamma (x+1)} e^{\frac{i \pi x}{2}} dx = -1.33432 - 0.125029 i.$

Question:

• Could someone give me a clue how to solve such an integral in complex domain?
• Does this type of integral occur more often: and what are it's applications?

This question arises from a debate I have for some years with people who believe pi is related to the golden ratio. I debate and argue why that is not the case. The latest analysis gave this formula. As math amateur I am looking for more insight (1).

import matplotlib.pyplot as plt
import numpy as np
from scipy.special import factorial
from scipy.special import gamma
Define layout spectrogram plot and time series
layout = [  ["xy_discrete", "sumxy_discrete"],  ["xy_continous", "sumxy_continuous"]  ]
gs_kw = dict(width_ratios=[1, 1], height_ratios=[1, 1])
fig, axd = plt.subplot_mosaic(layout, figsize=(12, 12), layout="constrained", gridspec_kw=gs_kw)
k = np.arange(50)

r = (np.pi)*k / factorial(k)
x = r  np.cos(np.pi * k / 2)
y = r * np.sin(np.pi * k / 2)
axd["xy_discrete"].plot(x, y, color="black", linewidth=1)
axd["xy_discrete"].plot(x[0], y[0], color="black", marker="o", fillstyle="none")
axd["xy_discrete"].annotate('start: [' + str(x[0]) +", " +  str(y[0]) + "]",
xy=(x[0], y[0]), xycoords='data', xytext=(2, 5), textcoords='offset points')
axd["xy_discrete"].plot(x[-1], y[-1], color="black", marker="o")
axd["xy_discrete"].annotate('stop: [' + str(np.round(x[-1],1)) +", " +  str(np.round(y[-1],1)) + "]",
xy=(x[-1], y[-1]), xycoords='data', xytext=(2, 15), textcoords='offset points')
axd["xy_discrete"].set_xlabel("x")
axd["xy_discrete"].set_ylabel("y")
axd["xy_discrete"].axis("equal")
axd["xy_discrete"].title.set_text('Discrete k: values')
sumx = np.cumsum(x)
sumy = np.cumsum(y)
axd["sumxy_discrete"].plot(sumx, sumy, color="black", linewidth=1)
axd["sumxy_discrete"].plot(sumx[0], sumy[0], color="black", marker="o", fillstyle="none")
axd["sumxy_discrete"].annotate('start: [' + str(np.round(sumx[0],1)) +", " +  str(np.round(sumy[0],1)) + "]",
            xy=(sumx[0], sumy[0]), xycoords='data', xytext=(-25, -15), textcoords='offset points')
axd["sumxy_discrete"].plot(sumx[-1], sumy[-1], color="black", marker="o")
axd["sumxy_discrete"].annotate('stop: [' + str(np.round(sumx[-1],1)) +", " +  str(np.round(sumy[-1],1)) + "]",
            xy=(sumx[-1], sumy[-1]), xycoords='data', xytext=(2, 15), textcoords='offset points')
axd["sumxy_discrete"].set_xlabel("x")
axd["sumxy_discrete"].set_ylabel("y")
axd["sumxy_discrete"].axis("equal")
axd["sumxy_discrete"].title.set_text('Discrete k: sum')

step = 0.01
k = np.arange(0, 50, step)

r = (np.pi)*k / gamma(k + 1)

x = r  np.cos(np.pi * k / 2)

y = r * np.sin(np.pi * k / 2)
axd["xy_continous"].plot(x, y, color="black", linewidth=1)
axd["xy_continous"].plot(x[0], y[0], color="black", marker="o", fillstyle="none")
axd["xy_continous"].annotate('start: [' + str(x[0]) +", " +  str(y[0]) + "]",
            xy=(x[0], y[0]), xycoords='data', xytext=(15, 5), textcoords='offset points')
axd["xy_continous"].plot(x[-1], y[-1], color="black", marker="o")
axd["xy_continous"].annotate('stop: [' + str(np.round(x[-1],1)) +", " +  str(np.round(y[-1],1)) + "]",
            xy=(x[-1], y[-1]), xycoords='data', xytext=(15, 20), textcoords='offset points')
axd["xy_continous"].set_xlabel("x")
axd["xy_continous"].set_ylabel("y")
axd["xy_continous"].axis("equal")
axd["xy_continous"].title.set_text('Continuous x: values')
sumx = stepnp.cumsum(x)
sumy = stepnp.cumsum(y)
axd["sumxy_continuous"].plot(sumx, sumy, color="black", linewidth=1)
axd["sumxy_continuous"].plot(sumx[0], sumy[0], color="black", marker="o", fillstyle="none")
axd["sumxy_continuous"].annotate('start: [' + str(np.round(sumx[0],1)) +", " +  str(np.round(sumy[0],1)) + "]",
            xy=(sumx[0], sumy[0]), xycoords='data', xytext=(10, 5), textcoords='offset points')
axd["sumxy_continuous"].plot(sumx[-1], sumy[-1], color="black", marker="o")
axd["sumxy_continuous"].annotate('stop: [' + str(np.round(sumx[-1],4)) +", " +  str(np.round(sumy[-1],4)) + "]",
            xy=(sumx[-1], sumy[-1]), xycoords='data', xytext=(2, 15), textcoords='offset points')
axd["sumxy_continuous"].set_xlabel("x")
axd["sumxy_continuous"].set_ylabel("y")
axd["sumxy_continuous"].axis("equal")
axd["sumxy_continuous"].title.set_text('Continuous x: integral')
plt.show()

Answer 1

Some ideas that could be helpful.

The function $E(x) = \int_0^\infty \frac{x^t}{\Gamma(t+1)}dt$ is interesting on it's own as it would be a continuous version of the exponential power series $e^x = \sum_{n=0}^\infty \frac{x^n}{n!}$.

This function satisfies the following formula $$ E(x) = \frac{1}{x}e^{x} - \frac{1}{x}\int_{0}^{\infty}\frac{e^{-xt}}{t\{\pi^{2} + (\log t)^{2}\}}\,dt,\tag{1} $$ which is mentioned here on page 25 and with a proof on page 196, and which is also discussed here.

A similar formula, but more useful for us, is the following: $$ E(x)= e^x - \int_0^\infty \frac{e^{-xt}}{t(\pi^2+\log^2t)}\, dt. \tag{2} $$ Now, either the two formulas are both correct and the difference is in $``\{\}``$ denoting the fractional part in (1), or both $()$ and $\{\}$ are the same, and one of the formulas is incorrect (the difference stemming from $x^t$ or $x^{t+1}$ in the numerator in the integral defining $E(x)$).
Let's assume that (2) is correct. More information about it can be found here.

The proof uses the reflection formula of the Gamma function $\Gamma(z)\Gamma(1-z)=\frac{z}{\sin(\pi z)}$ and the Laplace transform of the sine $\mathcal{L}(\sin(a z)) = \int_0^\infty \sin(a z) e^{-sz}dz = \frac{a}{a^2 + s^2}$.

You want to solve $$ \int_{0}^{\infty} \frac{\pi^x}{\Gamma (x+1)} e^{\frac{i \pi x}{2}} \,dx $$ I suggest to go back to setting $$ \int_{0}^{\infty} \frac{(i\pi)^x}{\Gamma (x+1)}\, dx $$ instead, as this will easily fit into the above formula.
In fact, the value that we want to compute is $$ E(i\pi) = \int_{0}^{\infty} \frac{(i\pi)^x}{\Gamma (x+1)}\, dx = e^{i\pi} - \int_0^\infty \frac{e^{-i\pi t}}{t(\pi^2+\log^2t)}\, dt. $$ which is equal to $$ e^{i\pi} - \int_0^\infty \frac{\cos(t)}{t(\pi^2+\log^2t)}\, dt + i\int_0^\infty \frac{\sin(t)}{t(\pi^2+\log^2t)}\, dt. $$

I believe that there is no closed form of $$ \int_0^\infty \frac{e^{-i\pi t}}{t(\pi^2+\log^2t)}\, dt $$ and I am not sure if there are ways to compute it to a high precision when $x$ is a pure imaginary number (for $\mathfrak{Re}(x)>0$) it should be easy).
The issue is that the integral is not absolutely convergent, we have an oscillating integral that does converge, but with no (to me known) closed form.

---

EDIT: It should be noted that the function $E(x)$ is only defined for $x\geq 0$. While I feel that it shouldn't be hard to extend it to $\mathfrak{Re}(x)>0$, I am not so sure if it can be easily extended to $\mathfrak{Re}(x)\geq 0$. So my solution is not a solution per se, but a hint of a formula which should be proved.