3

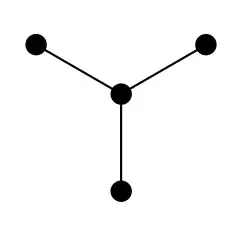
Below is an example of a 4-point graph from this book chapter that says it cannot be embedded isometrically into any $\mathbb R^n$.

enter image description here

I was thinking because of the following: The outer nodes are equidistant ($d=2$) from each other, so they must form an equilateral triangle in $\mathbb R^n$. Then the central node is equidistant from the outer nodes, so it must lie in the center of the triangle. However, the Pythagorean theorem would dictate that the distance from the center to the outer vertices would be $\sqrt 2 >1$, so this can't happen.

The only step I'm unsure about in this is what dictates that the central node would have to be in the center of the triangle. Is that actually true? Is there another proof technique that shows this result?

R. H. Vellstra
  • 3,263

1 Answers1

2

The central node would not have to lie at the center of the triangle; that's only true in $\mathbb R^2$. In $\mathbb R^3$, it would have to lie on a perpendicular axis through the center of that triangle, and in $\mathbb R^4$, there would be an entire plane of possibilities - and so on.

It can be shown, however, that the center of the triangle is the point where the central node would be closest to all three other points. And it's still not close enough - if the side length of the equilateral triangle is $2$, then the distance from the center to a vertex is $\frac23 \sqrt 3$, which is bigger than $1$.

Here's another argument: let $A, B, C$ be three of the nodes so that $B$ is the center node and $A,C$ are two of the outer nodes. Then in our desired embedding, $AB = BC = 1$ while $AC = 2$, so $AB + BC = AC$; this is only possible if $A,B,C$ are collinear with $B$ between $A$ and $C$.

If we replace $C$ by the fourth node, $D$, then the same argument says that $A,B,D$ are collinear with $B$ between $A$ and $D$, putting $D$ at the exact same location as $C$.

But then, $CD$ cannot equal $2$.

Misha Lavrov
  • 159,700