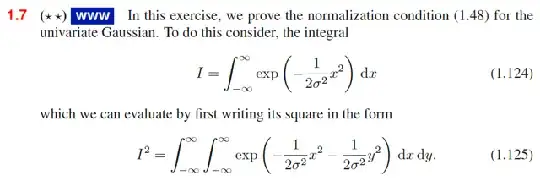Please help understand why the square $I^2$ of the integral of exponential$$ I = \int_{-\infty}^{\infty} exp(\frac {-1}{2\sigma^2} \, x^2) \, dx \tag{1} $$
can be expressed as double integral as in (2). $$ \begin{align} I^2 &= \int_{-\infty}^{\infty} exp(\frac {-1}{2\sigma^2} \, x^2) \, dx \int_{-\infty}^{\infty} exp(\frac {-1}{2\sigma^2} \, y^2) \, dy \\ &= \iint_{-\infty}^{\infty} exp \Bigl( \frac {-1}{2\sigma^2} \, (x^2 + y^2) \Bigl) \, \, dx \, dy \tag{2} \end{align} $$
I believe the product of integrals can be double integral because of exponential but could not understand how it can be transformed as such.
Pattern Recognition and Machine Learning