The question is
A street light is mounted at the top of a 15-ft-tall pole. A man 6 ft tall walks away from the pole with a speed of 5 ftys along a straight path. How fast is the tip of his shadow moving when he is 40 ft from the pole?
I drew a diagram like this to model the situation:
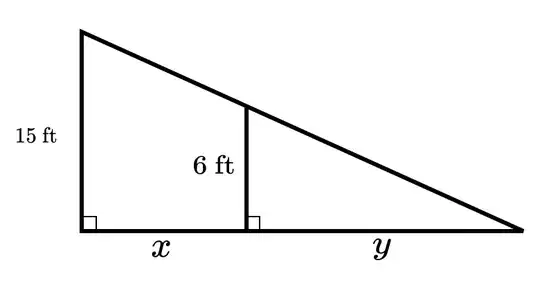
Where $x$ is the distance between the pole and the man, and $y$ is the length of the shadow of the man. I'm pretty sure the question is asking to find $\frac{dy}{dt}$ when $x=40$, so I expressed $y$ in terms of $x$. $$ \frac{15}{6}=\frac{x+y}{y} \Rightarrow y=\frac{2}{3}x $$ I tried using the chain rule to find $\frac{dy}{dt}$: $$ \frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt} $$
We're given that the man is walking at $5 \text{ ft/s}$ so $x$ is increasing at a rate of $5 \text{ft/s}$, therefore, $\frac{dx}{dt}=5$. To find $\frac{dy}{dx}$ we simply differentiate both sides of the equation with respect to $x$. $$ y=\frac{2}{3}x \Rightarrow \frac{dy}{dx}=\frac{2}{3} $$
So it follows that since $\frac{dx}{dt}=5$ and $\frac{dy}{dx}=\frac{2}{3}$, $\frac{dy}{dt}$ must be $$ \frac{dy}{dt} = \frac{dy}{dx}\frac{dx}{dt} = 5\cdot \frac{2}{3} = \frac{10}{3} \text{ ft/s} $$
Except that it isn't. The correct answer in the textbook I'm using states that it is in fact $\frac{25}{3} \text{ ft/s}$. I'm just confused about where I went wrong! This was my entire process to get to the incorrect answer.