solving the integral $ \int_0^\infty \dfrac{\sin xt}{x(x^2+1)} dx $

Question

How to solve the following integral by differential equations techniques? $$ \int_0^\infty \dfrac{\sin xt}{x(x^2+1)} dx $$

Answer 1

Recalling the Laplace transform

$$ F(s)=\int_{0}^{\infty} f(t) e^{-st} dt. $$

We can use it to solve the problem. Taking Laplace transform with respect to $t$ gives

$$ f(t)=\int_0^\infty \dfrac{\sin xt}{x(x^2+1)} dx \implies F(s)=\int_{0}^{\infty}\frac{dx}{(1+x^2)(s^2+x^2)} . $$

The last integral can be evaluated using partial fraction techniques (see below) to give

$$ \implies F(s) = \frac{1}{2}\,{\frac {\pi }{s \left( s+1 \right) }}. $$

Now, we can find the inverse Laplace transform using convolution technique as

$$ f(t)=\frac{\pi}{2}\int_{0}^{t} e^{-\tau}d\tau = \frac{\pi}{2}(1-e^{-t}). $$

Alternatively, one can use partial fraction technique

$$ \frac{\pi}{2}\frac {1}{s(s+1)}=\frac{\pi}{2}\left(\frac{1}{s}-\frac{1}{s+1}\right). $$

to find the inverse Laplace transform

Notes:

1) The Laplace transform of $\sin(az)$ with respect to $z$ is $$ {\frac {a}{{s}^{2}+{a}^{2}}}. $$

2) $$\frac{1}{(1+x^2)(s^2+x^2)}={\frac {1}{ \left( {s}^{2}+{x}^{2} \right) \left(1- {s}^{2} \right)}}-{\frac {1}{ \left( {x}^{2}+1 \right)\left(1- {s}^{2} \right) }}.$$

3) Inverse Laplace transform of $\frac{1}{s}$ and $\frac{1}{1+s}$ are given by $$ 1,\quad e^{-t} $$ respectively.

Answer 2

This integral is custom-made for analysis via integration in the complex plane. I'm not sure if you have any familiarity with the following concepts (e.g., residues), but I am going to evaluate it here in this fashion for completeness.

Consider the following integral in the complex plane:

$$\oint_C dz \frac{e^{i z t}}{z (z^2+1)}$$

where $C$ is the following contour:

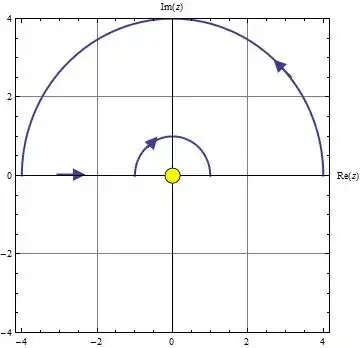
Thus, we avoid the pole at $z=0$ by deforming into the upper half plane. The contour integral is thus equal to

$$\int_{-R}^{-\epsilon} dx \frac{e^{i x t}}{x (x^2+1)} + i \epsilon \int_{\pi}^0 d\phi \, e^{i \phi} \frac{e^{i \epsilon e^{i \phi} t}}{\epsilon e^{i \phi} (\epsilon^2 e^{i 2 \phi}+1)}+ \\ \int_{\epsilon}^{R} dx \frac{e^{i x t}}{x (x^2+1)} +i R \int_0^{\pi} d\theta \, e^{i \theta} \frac{e^{i R e^{i \theta} t}}{R e^{i \theta} (R^2 e^{i 2 \theta}+1)} $$

We take the limit as $\epsilon \to 0$ and $R \to \infty$. Note that the second integral becomes $-i \pi$. The fourth integral vanishes when $t \gt 0$; its magnitude is bounded by

$$\frac{2}{R^2} \int_0^{\pi/2} d\theta \, e^{-R t \sin{\theta}} \le \frac{2}{R^2} \int_0^{\pi/2} d\theta \, e^{-2 R t \theta/\pi} \le \frac{\pi}{R^3 t}$$

On the other hand, the contour integral is equal to, by the residue theorem, $i 2 \pi$ times the residue at the pole $z=i$ (i.e., the only pole within the contour $C$). Thus

$$PV \int_{-\infty}^{\infty} dx \frac{e^{i x t}}{x (x^2+1)} - i \pi = i 2 \pi \frac{e^{-t}}{2 i^2} $$

or

$$PV \int_{-\infty}^{\infty} dx \frac{e^{i x t}}{x (x^2+1)} = i \pi \left ( 1 - e^{-t}\right )$$

Now, take the imaginary part of both sides; the principal value disappears and we get, for $t \gt 0$:

$$\int_{0}^{\infty} dx \frac{\sin{ x t}}{x (x^2+1)} = \frac{\pi}{2} \left ( 1 - e^{-t}\right )$$

Answer 3

In order to get rid of the term x in the denominator, we use Feynman’s trick using the parametrised integral $$ I(t)=\int_0^{\infty} \frac{\sin (tx)}{x\left(1+x^2\right)} d x $$ Differentiating $I(t)$ w.r.t. $t$ yields $$ I^{\prime}(t)=\int_0^{\infty} \frac{\cos (tx)}{x^2+1} d x $$ Using contour integration along anti-clockwise direction of the path $$\gamma=\gamma_{1} \cup \gamma_{2} \textrm{ where } \gamma_{1}(t)=t+i 0(-R \leq t \leq R) \textrm{ and } \gamma_{2}(t)=R e^{i t} (0<t<\pi) $$ $$ \begin{aligned} \int_0^{\infty} \frac{\cos (tx)}{x^2+1} d x &= \Re \int_0^{\infty} \frac{e^{x t i}}{x^2+1} d x\\&=\frac{1}{2} \int_{-\infty}^{\infty} \frac{e^{x t i}}{x^2+1} d x \\&=\\ & =\frac{1}{2} \cdot 2 \pi i\left(\lim _{z \rightarrow i}(z-i) \frac{e^{z t i}}{z^2+1}\right) \\ & =\pi i \cdot \frac{e^{i \cdot t i}}{2 i}\\&=\frac{\pi e^{-t}}{2} \end{aligned} $$ Integrating back, we have $$ \begin{aligned} I(t) & =I(t)-I(0)\\&=\int_0^t \frac{\pi e^{-a}}{2} d a \\ & =\frac{\pi}{2}\left(1-e^{-t}\right) \end{aligned} $$

Answer 4

Hint: Let $$ y(t)=\int_0^{\infty} \frac{\sin (tx)}{x\left(1+x^2\right)} d x. $$ Then, $$\ddot{y}-y=-\frac{\pi}2.$$ The solution is $$y(t)=\frac{\pi}2+c_1e^t+c_2e^{-t}$$ with initial conditions $y(0)=0$ and $\dot y(0)=\frac{\pi}2$.