Moran's theorem Open set condition Koch Curve

Question

I am currently studying some measure theoretic fractal geometry, and I am trying to learn how to use Moran theorem. The statement I currently have is:

Moran's theorem:

if $F_1,...,F_N : \mathbb{R}^d \to\mathbb{R}^d $ such that $|F_i(x) - F_i(y)| = r_i |x-y|$ where each $r_i \in (0,1)$, and there exists an open set $U$ such that $F_i(U) \subseteq U$ for all $i \in [N]$ and $F_1(U), ...,F_N(U)$ are disjoint then:

(I) There exist unique non-empty compact set $K$ such that $K = F_1(U) \cup .... \cup F_N(U)$

(II) There exists unique $\alpha$ sucht that $H^\alpha(K) \in (0, \infty)$ where $\alpha$ is determined by $r_1^\alpha + ... + r^\alpha_N = 1$

Using Moran's theorem

The classical example application is the cantor set. For this case we consider the contractions $F_1(x) = x/3$ and $F_2(x) = x/3+ 2/3$, and the open set $(0,1)$ we see that indeed all the conditions are met and $r_1 = r_2 = 1/3$, therefore the Hausdorff dimension of the cantor set satisfies : $2(1/3)^\alpha = 1 \implies \alpha = \log(2)/\log(3)$

My question + Koch's curve

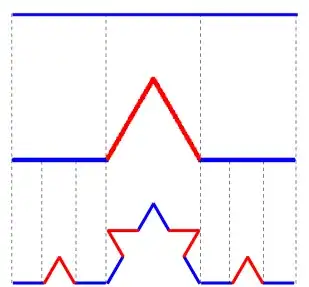
Consider the Koch curve: Basically we take the unit interval slit it in 3 parts of length $1/3$ and in the middle one we construct an equilateral triangle, and keep everything but the base, here is a picture:

My intuition and half cooked solution. My intuition is that we are simply going to be shrinking by $1/3$, and we do this four times every time, therefore the contractions will all have $r_i = 1/3$ and therefore the Hausdorff dimension of the Koch's curve should be $4(1/3)^\alpha \implies 4 = 3^\alpha \implies \alpha = \log(4)/ \log(3)$.

The problem:

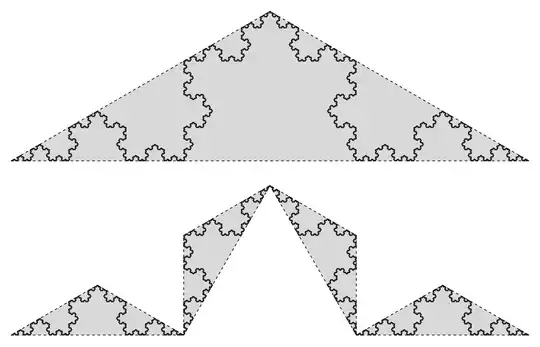
$\color{red}{\textbf{What is my Open set?}}$

I found a website that has the explicit contractions ( I also stole the picture from there)

https://larryriddle.agnesscott.org/ifs/kcurve/kcurve.htm

But even with this information I cannot figure out what my open set should be.

Thank you for the help in advance. I would also appreciate any other examples of fractals that you might want to give me, I want to get good at this. Thank you!!

Answer 1

For the Koch Curve, one possible choice for the open set $U$ is the interior of the triangle with vertices $$ (0,0), (1,0), \text{ and } (1/2,\sqrt{3}/6): $$

In general, though, $U$ need not be a simple set; it can be as complicated or even more complicated, than the fractal attractor itself. As an illustration, you might consider trying to find the open set for the IFS: $$ \begin{aligned} f_1(x,y) &= \frac{1}{2} \left( \begin{array}{cc} 1 & -1 \\ 1 & 1 \\ \end{array} \right) \left( \begin{array}{cc} x \\ y \\ \end{array} \right) \\ f_2(x,y) &= \frac{1}{2} \left( \begin{array}{cc} 1 & -1 \\ 1 & 1 \\ \end{array} \right) \left( \begin{array}{cc} x \\ y \\ \end{array} \right) + \left( \begin{array}{cc} 1 \\ 0 \\ \end{array} \right). \end{aligned} $$ The attractor of the IFS broken into two parts with the boundary between the highlighted looks like so: This set (called the twin-dragon) is two-dimensional. The logical open set to use is exactly the interior of the set. Describing the interior requires describing the boundary, which is arguably more complicated that describing the original set itself.

For this reason, there are other, algebraic criteria which are often more useful. Here are a couple of research papers on that topic:

• Integer matrices and fractal tilings by Christoph Bandt
• Weak separation properties for self-similar sets by Martin Zerner