-1

Consider the RDE $$X_t = \int_0^t e^{cW_s}ds$$ where $c>0$ and $W_t$ is Wiener process. Can this integral be solved, i.e. can Wiener process be integrated w.r.t. time?

Now consider the integral $$X_t = \int_0^t sin(s)dB_s.$$ This integral cannot be further solved, is this correct?

Sinem
  • 43
  • 1
    Does this answer your question? https://math.stackexchange.com/questions/72208/whats-the-difference-between-rde-and-sde – Kamal Saleh Sep 22 '22 at 15:02
  • Stochastic differential equations? – Benjamin Wang Sep 22 '22 at 15:02
  • 1
    Do you mean $y'(x)=f(x,y(x),p)$ and the parameters $p$ get randomly selected? Or that the coefficients vary randomly in time? – Lutz Lehmann Sep 22 '22 at 15:05
  • 1
    What do you mean with a "random differntial equation" ? An arbitary equation involving derivates ? – Peter Sep 22 '22 at 15:31
  • Assuming that $B$ is also a Brownian motion the integral $\int_0^t\sin(s),dB_s$ has nothing to do with the title of your question. It cannot be further solved but it can be related to the integral $\int_0^t B_s\cos s,ds$. Hint: integration by parts. – Kurt G. Sep 26 '22 at 09:28

2 Answers2

1

  • The correct way to write this equation is either $$ X_t=\int_0^te^{cW_\color{red}{s}}\,d\color{red}{s} $$ or -in differential form- $$ dX_t=e^{cW_t}\,dt\,. $$ It looks like you mixed up both.

  • This integral is well defined even as a Riemann integral because for each $\omega$ the path $t\mapsto W_t(\omega)$ is continuous.

  • It cannot be solved like we solve $$ \int_0^te^{cs}\,ds=\frac{e^{ct}-1}{c}\, $$ but this has not stopped generations of mathematicians to work with such integrals in the theory of stochastic differential equations or financial mathematics.

For example: Since Black & Scholes it is popular to model a stock price essentially by $$ S_t=S_0e^{cW_t-c^2t/2}\,. $$ Then $$ X_t=\frac{1}{t}\int_0^tS_s\,ds $$ describes the average stock price which is the underlying of an Asian option.

Kurt G.
  • 17,136
0

This is a Random differential equation, which differs from a Stochastic differential equations.

An RDE (or RODE) is an (path-wise) ODE containing a random process, in this case a Wiener process. Because of this, in a path-wise sense, the solution can be handled using standard (deterministic) calculus.

An SDE (driven by standard Brownian motion) is an equation of the form

$$dX_t = f(t,X_t)dt + g(t,X_t)dW_t,\,\, W_t : \text{ Wiener process}$$ Your notation is incorrect, you are mixing differential and integral forms.

$$\frac{dX_t}{dt} = e^{cW_t} \text{ or } X_t = \int_0^t e^{cW_s}ds$$

An aside: Interestingly, calling them stochastic differential equations is a bit of a misnomer, since sample paths are nowhere differentiable, so really they are stochastic integral equations.

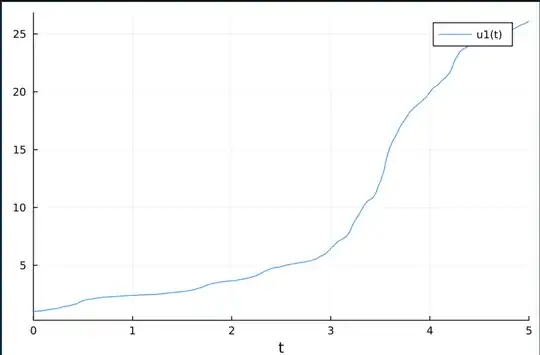
Here is one numerical solution using Julia programming language with initial condition $X_0 = 1.0$ and $c = 2.0$ (cf. Julia DiffEq)

enter image description here

I recommend the following book Random Ordinary Differential Equations

EDIT: OP has added a stochastic integral question below original RDE question, for such integrals I recommend the following book: Stochastic Differential Equations

oliverjones
  • 4,289
  • So how to compute this solution then? – Sinem Sep 26 '22 at 08:44
  • I said an RDE is an ODE defined path-wise, thus for a given realization, we may solve it using deterministic calculus, i.e. sans probability. The caveat is though this is path-wise, so each realization will be different with a positive probability. – oliverjones Sep 26 '22 at 15:08