1

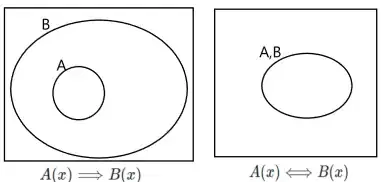
Suppose that $A(x) $ is the proposition $x^{2}=25,$ and $B(x)$ is the proposition $x\leqslant 10.$ How can I show for all $x\in \mathbb{R}$ that $A(x) \Rightarrow B(x)$ is always true?

I understand that if the implication is true there cant exist any case where $A(x) $ is true and $B(x)$ is false. My question is how do i prove this formally and mathematically correct? And also is there any way to visualise propositions like this in a Venn-diagram?

ryang
  • 44,428
evolhart
  • 81
  • This really isn’t a problem in propositional logic:: the statement isn’t true solely because of how the atomic statements are connected by logical connectives ($\implies, \neg, \land$, and so on). As you state, you want to prove the statement for all reals. Implicitly, the whole formula is wrapped in a universal quantifier $(\forall x)$ — or, better, $(\forall x\in \mathbb{R})$. – BrianO Aug 29 '22 at 07:08

2 Answers2

3

Suppose that $A(x) $ is $x^{2}=25,$ and $B(x)$ is $x\leqslant 10.$

is there any way to visualise propositions like $$\forall x{\in}\mathbb{R}\,\Big(A(x) \Rightarrow B(x)\Big)$$ in a Venn-diagram?

Take any $x.$ Satisfying $x^{2}=25$ implies that it also satisfies $x\leqslant 10.$ This means that the solution set of the first equation is a subset of the solution set of the second equation. (left diagram)

This subset is improper (that is, the two equations have the same solution set) if and only if, in fact, $\forall x{\in} \mathbb{R}\,\Big(A(x) \Leftrightarrow B(x)\Big).$ (right diagram)

![![enter image description here

My previous answer elaborates on this.

ryang
  • 44,428
2

Lets first take a close look at proposition $A(x): x^2=25$. This proposition implies $A'(x): x = \pm 5$. Then, since $\pm 5 \leq 10$, proposition $B(x): x \leq 10$ follows.

Indeed, you can look at proposition $A(x)$ as being a subset of proposition $B(x)$, $A(x) \subset B(x)$. I.e., considering $B(x)$ as being the set of all values less or equal than $10$, and $A(x)=\{-5, +5\}$ (the values of $x$ that make the statement true), $A(x)$ can be thought as a proper subset of $B(x)$.

tomate
  • 119