Surprising Patterns in Numbers whose Digit Sum is equal to their Square Root in an arbitrary Base.

Question

In base 10, $\sqrt{81} = 8 + 1 = 9$. It turns out that 81 is the only number in base 10 that has this property. I wanted to find out if there are other numbers with this property in other bases. Mathematically, for a given base $b$, I'm looking for numbers $n$ with digits $d_i$ in base $b$ such that

$$ \sqrt{\sum^{\infty}_{i=0} d_i\cdot b^i} = \sum^{\infty}_{i=0} d_i $$

I wrote this code to brute force the solutions in any given base. I've also uploaded the set of solutions for the first 5000 bases here. Here I don't consider 0 and 1 to be solutions

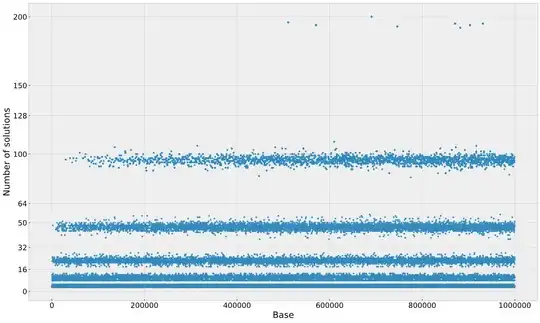
The pattern arises when I tried [plotting the number of solutions for 1 million bases (plot only includes at most 5000 data points from each strip $[2^n, 2^{n+1}]$):

There are distinct gaps in the data that appears to roughly correlate with powers of 2? Furthermore, the smallest base of each "strip" are bases 7, 31, 211, 2311, 30031, 510511, which are Euclid numbers, these bases have 5, 10, 21, 48, 96, and 196 solutions respectively. I've verified that base 9699691 has 397 solutions and base 223092871 has 784 solutions. Here's the data in numpy.array format

I'm not quite sure what to make of this. On the one hand, the powers of two-like pattern makes me suspect that it could stem from a floating point precision error or a bug in the code. On the other, the manner in which the powers of two present themselves feels atypical for a computational error.

My question is does this pattern actually exist, and if so I would appreciate any insight into why such a pattern arises from this problem.

Edit: It also appears that $(b-1)^2$ is always a solution as proven in the comments.

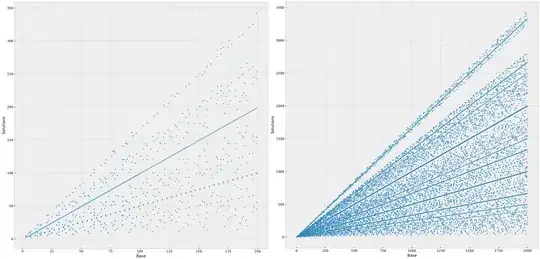
Edit 2: I plotted out the solutions $\sqrt{n}$ against the base $b$, and there appears to be rays with varying slopes:

Answer 1

I've actually already spent a while thinking about this topic, since it appeared on the 2022 Mathcamp qualifying quiz.

One of the useful things to keep in mind here is that the digit sum of $n^2$ in base $b$ is congruent to $n^2$ modulo $b-1$. (Being a perfect square is nothing special here.) In base $10$, we know this as the divisibility rule by $9$, but it generalizes to all bases. So if the digit sum of $n^2$ in base $b$ is equal to $n$, then we have $$n^2 \equiv n \pmod {b-1}.$$

This is not an if-and-only-if condition in general. It becomes one in a special case:

Lemma. If $n<b$ and $n^2 \equiv n \pmod{b-1}$, then the sum of digits of $n^2$ is $n$.

Proof. In this case, $n^2 < b^2$, so $n^2$ is a two-digit number in base $b$. The sum of digits of $n^2$ in that case is at most $2(b-1)$, and it's congruent to $n$ modulo $b-1$. Therefore there are only two things that the sum of digits of $n^2$ can be: $n$, or $n+b-1$. Now we must rule out $n+b-1$.

The sum of digits of $n^2$ in the two-digit case is $n^2 - (b-1)\lfloor \frac{n^2}{b}\rfloor \le n^2 - (b-1) \cdot \frac{n^2-b-1}{b} = \frac{n^2 + (b-1)^2}{b}.$ So for the sum of digits to be $n+b-1$, we'd need $n+b-1 \le \frac{n^2 + (b-1)^2}{b}$, which simplifies to $nb \le n^2-b$. However, in fact, $nb > n^2$ because $n < b$ by assumption. Therefore the sum of digits can only be $n$. $\square$

---

This explains why we have a rich collection of solutions when $b = p_1 p_2 \cdots p_k + 1$ for primes $p_1, p_2, \dots, p_k$. In such a case, we have $2^k$ solutions $n^2$ with $n<b$ due to the lemma above.

To find them, note that $n^2\equiv n \pmod {p_i}$ has two solutions: $n \equiv 0 \pmod{p_i}$ or $n \equiv 1 \pmod{p_i}$. There are $2^k$ ways to to mix and match these options for $i=1, 2,\dots, k$, and then we can combine them into a solution modulo $b-1 = p_1 p_2 \cdots p_k$ by the Chinese remainder theorem. (Two of them are $n=0$ and $n=1$, which we may decide to ignore; however, $n=0$ also gives us $n=b-1$, which is always a solution.)

We're likely to get some other solutions as well. For example, when $b=7 = 2\cdot 3+1$, we get the solutions $1^2, 3^2, 4^2, 6^2$ in this way: the digits of $1^2=1=1_7$, $3^2=3=12_7$, $4^4=16=22_7$, and $6^2=36=51_7$ sum to $1, 3, 4, 6$ respectively. There are also two more solutions, $9^2$ and $12^2$, which appear for other reasons.

However, the other solutions can't be too frequent. In general, the sum of digits of $n^2$ is at most $(b-1)(1 + \log_b n^2)$, which is eventually guaranteed to be smaller than $n$. Working with this inequality for a bit, we can deduce: first, that for large $b$, $n^2$ has at most three base-$b$ digits; second, that for large enough $b$, $n < 2b$. (Better bounds exist.) Also, we still have to satisfy $n^2 \equiv n \pmod{b-1}$ for $n\ge b$, even if it's no longer a sufficient condition. So while there are at least $2^k$ solutions, there are fewer than $2^{k+1}$, and probably significantly fewer.

For general $b$, we see the same pattern, with $k$ replaced by the number of distinct prime factors of $b-1$. (In the Chinese remainder theorem, we get to factor $b-1$ into distinct prime powers, and then mix and match solutions to $n^2 \equiv n$ modulo each prime power.) Since $b = p_1 p_2 \cdots p_k + 1$ is the smallest base for which $b-1$ has $k$ distinct prime factors, it is the smallest base for which we can hope to get $2^k$ solutions, so it is record-setting.