I know Derivatives can be defined on functions.My question is can we defined derivative on arbitrary relation?if not then whats the problem with it?(2) why we defined derivative only on real number ,i mean what are requirement to define it on arbitrary topological vector space?
Asked
Active
Viewed 93 times
2
-
2There are many notions of derivatives that generalise the usual notion from real analysis. In general there is no most general notion: i.e. the generalisations are pretty specific and use machinery from the more abstract contexts they are defined upon. This includes there being made different definitions for derivatives upon TVSs. I don't think anyone has generalised derivatives from functions to relations, and I do not think that avenue of inquiry will be massively fruitful, at least in the context of analysis. – user2628206 Jul 27 '22 at 05:34
-
1Related are three of the answers to Calculus and Category theory -- answer 1 and answer 2 and answer 3. – Dave L. Renfro Jul 27 '22 at 08:16
-
As a general rule (you can break it if you need to, but it makes life harder), differentiation is defined on complete topological vector spaces, as it allows the limit to exist when it behaves like it is converging. – Paul Sinclair Jul 28 '22 at 03:49
1 Answers
1
There are no derivatives but there are differentials defined e.g. the Gateaux differential and the Frechet differential . The Gateaux differential is defined on locally convex topological vector spaces:
$D(f,x_{0},v)=\displaystyle \lim_{\epsilon \to 0}\dfrac{f(x_{0}+\epsilon\,v)-f(x_{0})}{\epsilon}$
where $v$ is the direction of the differential.
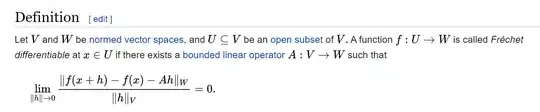
The Frechet derivative is defined only in Normed Vector Spaces as follows:
As you can see the Frechet differential is independent of direction!
-
Can i consider our usual differential on set of real number as a part Frechet differential with usual norm? – MEET PATEL Jul 27 '22 at 05:57
-
If you have an open set $U$ and $x_{0}$ in $U$ , yes! If the function is real then you get $A=f'(x_{0})$ – Jul 27 '22 at 06:00
-
@GeorgeTsoutsinos, what's the difference between the Frechet differential and the Jacobian matrix? Only that the former is more general i.e. can be used on maps other than $\Bbb{R}^n\to \Bbb{R}^m$? – Sebastián P. Pincheira Jul 27 '22 at 06:41
-
No. I think the Jacobian is defined only for$ f:\mathbb{R^{m}}\to \mathbb{R^{n}}$. – Jul 27 '22 at 06:56
-
Mr. Downvoter I say it plainly! Gateaux on locally convex TVS and Frechet on normed vector spaces! I don't see the point of your downvote! – Jul 28 '22 at 06:14