Projection of a cylinder from XYZ 3D space on to XY plane.

Question

A cylindrical body of length $ \ L \ $ lies in the XYZ 3D space. The base of the cylinder makes an angle $\psi$ with the Z axis, as shown in image link. I would like to know the projection of that cylinder in the XY plane in terms of length and azimuthal angle $\psi$.

Where did you come across this? What do you think? How would you start? What level of 3D geometry are you comfortable with? Your question is currently an “isolated problem”, i.e. it doesn’t answer any o the above, essentially stating, “here’s the question, solve it for me”. These questions generally tend to attract negative attention and get closed quickly. So it is in your best interests to artain a comprehensive answer, that you edit the post to answer all of the following, and make sure to include your own attempts. — insipidintegrator, Jul 18 '22 at 14:56
$\psi$ shown in the figure is not the azimuthal angle. The azimuthal angle is the angle between the projection of the a vector in $3D$ onto the $XY$ plane, and the the $X$ axis. — , Jul 19 '22 at 08:18
You have used $\psi$ as a symbol for one of the input values of the problem, and also as a symbol for one of the output values of the problem. Do you see where you went wrong? — David K, Jul 24 '22 at 23:02
When you use the word "line" people will usually think of an line that extends indefinitely. To specify an object that starts at one point, goes straight to another point, and ends at the other point, use the term "line segment". Writing about a cylinder when you actually just want a line segment makes the question far more complicated. — David K, Jul 24 '22 at 23:08

score 2 · Accepted Answer · 2022-07-19T10:48:50.930

Let $u = (u_x, u_y, u_z)$ be the unit vector along the axis of the cylinder, with $u_z \gt 0$. And let $C$ be the center of the lower base of the cylinder, and let $R$ be the radius of the bases.

Generate two vectors $v_1 $ and $v_2$ with $v_1$ horizontal, that are orthogonal to the axis unit vector $u$. Hence,

$ v_1 = (u_y, -u_x, 0 ) / \sqrt{u_x^2 + u_y^2} $

Then it follows that

$ v_2 = u \times v_1 = (u_x, u_y, u_z) \times (u_y, - u_x, 0) / \sqrt{u_x^2+ u_y^2} = (u_x u_z, u_y u_z, -(u_x^2 + u_y^2) ) / \sqrt{u_x^2 + u_y^2} $

The boundary of the lower base is the ellipse

$ P_1(\theta) =\text{Proj}(C) + R \cos(\theta) \text{Proj}(v_1) + R \sin(\theta) \text{Proj}(v_2) \hspace{50pt} 0 \le \theta \le \pi $

This simplifies to

$ P_1(\theta) = (C_x, C_y) + \dfrac{1}{\sqrt{u_x^2 + u_y^2}}\bigg( R \cos(\theta) (u_y, - u_x) + R \sin(\theta) (u_x u_z, u_y u_z) \bigg) \hspace{50pt} \theta \in [-\pi, 0] $

Similarly the projection of the upper base is

$P_2(\theta) = (C_x + L u_x, C_y + L u_y ) +\dfrac{1}{\sqrt{u_x^2 + u_y^2}}\bigg( R \cos(\theta) (u_y, - u_x) + R \sin(\theta) (u_x u_z, u_y u_z) \bigg) \hspace{50pt} \theta \in [0 , \pi ] $

Finally we have the boundary of the projection of lateral surface of the cylinder, and this is a couple of line segments, given as follows

$P_3(t) = (C_x , C_y) + \dfrac{R}{\sqrt{u_x^2 + u_y^2}}( u_y, - u_x ) + t L (u_x, u_y) \hspace{50pt} t \in [0, 1] $

and

$P_4(t) = (C_x, C_y) - \dfrac{ R}{\sqrt{u_x^2 + u_y^2}}( u_y, - u_x ) + t L (u_x, u_y) \hspace{50pt} t \in [0, 1] $

The segments $P_1, P_2, P_3, P_4 $ define the boundary of the projection of the cylinder.

The above is seen on this GeoGebra graphic which I prepared.

Thanks for such a detailed mathematical solution. I would like to know what would be the projection in the XY plane if we replace the cylinder with a line in the above analysis. Shall that be simply $Lsin\phi$ in XY plane? — rohit kumar singh, Jul 19 '22 at 11:22
Yes. In this case you can ignore $P_1$ and $P_2$, and then the segments $P_3$ and $P_4$ become the same segment, as $R=0$ — , Jul 19 '22 at 12:37

score 1 · Answer 2 · answered Jul 24 '22 at 14:24

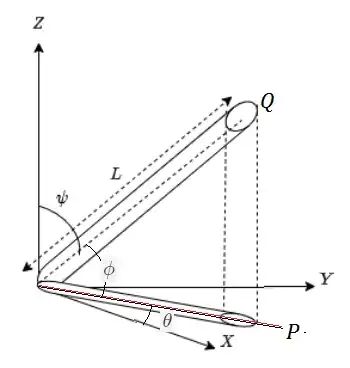
For better nomenclature in spherical coordinates, $(\theta,\phi, \psi)$ are azimuth or longitude , latitude or elevation and co-latitude respectively.

$$ \psi+\phi= 90^{\circ};\quad $$

Origin O, $X,Y,Z$ are Cartesian coordinate axes. $OP$ is simple direct projection of $L$ on horizontal plane $YOX,$ (treating the tube as a line through the origin)

$$ OP= L \cos \phi = L \sin \psi. $$

Projection of a cylinder from XYZ 3D space on to XY plane.

2 Answers2

Linked