I have a family of rational maps $f$ ( the Blaschke fraction ) with one complex parameter $\rho$:
$$f(z) = \rho z^2 \frac{z-3}{1-3z}$$
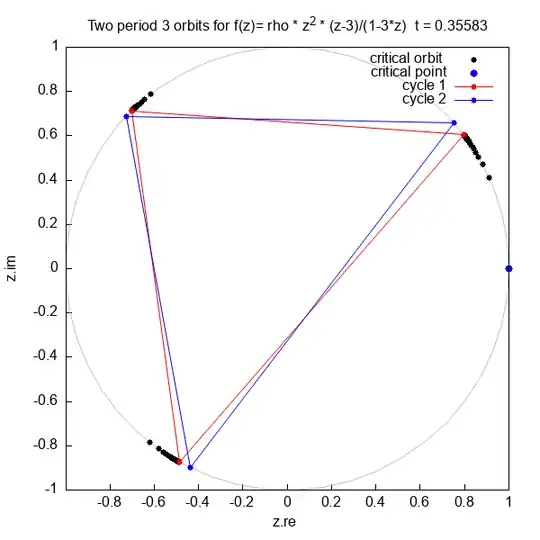
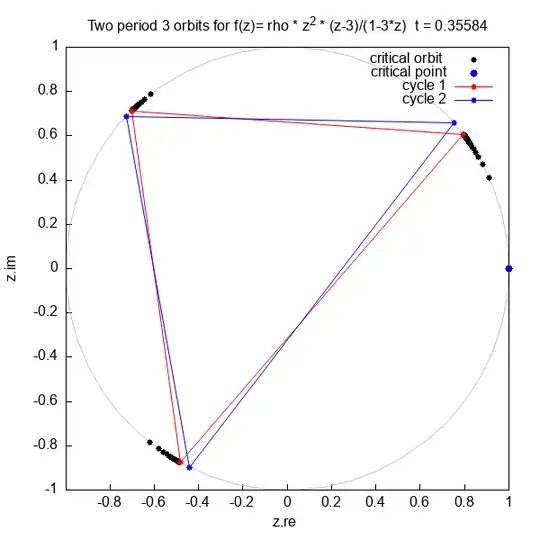
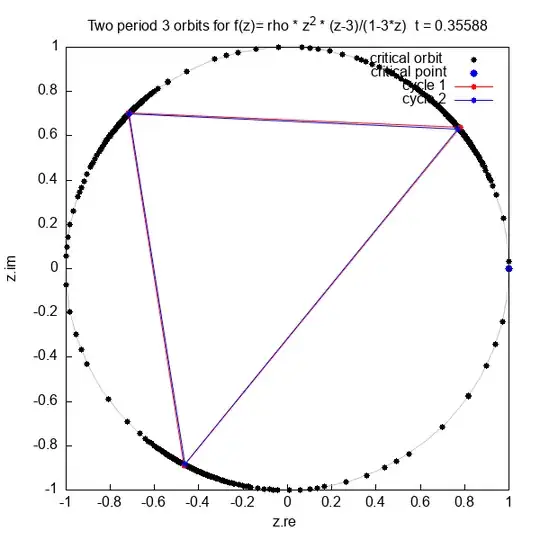
I want to find $\rho$ such that map $f$ has a parabolic period 3 cycle on the unit circle.
So $\rho$ should be a solution of system of equations:
$$ \begin{cases}f^3(z_0) = z_0 \\ |(f^3)'(z_0)| = 1 \end{cases}$$
where
- $f^3(z) = f(f(f(z)0)))$ is 3-rd iteration of function f
- $(f^3)'(z_0)$ is the first derivative of $f^3$ with respect to $z$ at $z_0$
- $z_0$ is the point from period 3 parabolic cycle
but computing derivative of iterated function is hard
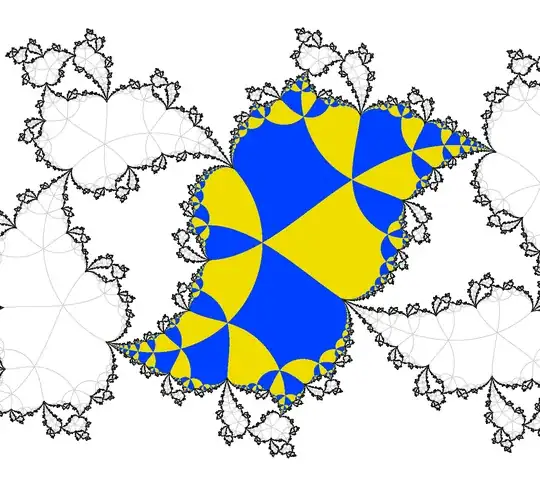
The image of dynamic plane with Julia set:
It is fig 3 from paper : Near Parabolic Renormalization for Unicritical Holomorphic Maps by Arnaud Chéritat
I know that $\rho$ has a modulus equal to one (complex number):
$$ |\rho| = 1 $$
My first try was easy solution ( point on the unit circle with angle in turns = 1/3)
$$ \rho = e^{2 \pi i / 3} = -0.5 +0.8660254037844386 i$$
Then the period 3 cycle is on the unit cirlce but the cycle is not parabolic and the image is different.
Q. How can I find such $\rho$ using algebra or numerical root finding ? How can I solve above system of equations ?