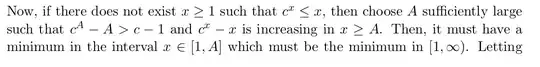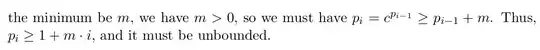For a given $c$ define the power tower $p$ of $c$ as follows: $$p_0 = 1,~~p_i = c^{p_{i−1}} . $$ Find the largest $c$ such that this sequence is bounded.
Clearly $c=1$ works. So assumer $c>1.$ Note that for $c>1,$ $c^n$ is increasing as $n$ increases.
There are two cases:
- There exists $x\ge 1$ such that $c^x\le x$
- There does not exist $x\ge 1$ such that $c^x\le x$
Note that if there exists $x\ge 1$ such that $c^x\le x$ and hence we get the sequence $\{c^n\}$ to be bounded above by $x.$ Since $\{c^n\}$ is bounded above then so is $\{p_i\}.$
But I couldn't understand the following part.
After this we have to find the maximum value of $c$ such that there exist $x$ such that $c^x\le x\implies x^{1/x}\le c$ or find maximum value of $c$ which is ( after differentiating) we get $e^{1/e}.$
My doubt is, I get that $c^x-x$ is increasing but it might be bounded above so how can we say that there exists $A$ such that $c^A>A+c-1$ ( we know that $c^x>x$ for all $x>1$).
Moreover, if $c^x-x$ is increasing, then in the interval $[1,A]$ wouldn't $c-1$ be the minimum?
And lastly, I did not understand how $p_i=c^{p_{i-1}}\ge p_{i-1}+m.$ But I understood that if $p_i=c^{p_{i-1}}\ge p_{i-1}+m$, then we must have $p_i\ge 1+m\cdot i.$
Any help or other solution is appreciated.