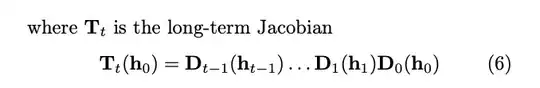1

I am reading a paper using random matrix theory to calculate Lyapunov spectrum.

What particularly confuses me is

1.

a

Why with $h_i \sim \mathcal{N}(0, \Delta_0), \phi = \tanh$, can we have $p(y)$ as the above integral? I.e. how to calculate the probability density of a function of a variable with known distribution?

(This seems to follow from basic probability theory, though I am not sure why there is a $\delta$ function.)

2.

I am too much confused by this step..

b

Why is the Lyapunov spectrum simply the inverse of $\chi(x)$ (the probabilistic eigenvalue distribution of the Jacobian $D_{ij}(t_s)$)? Moreover, shouldn't it be the Oseledets $\Lambda$ instead of $D_{ij}(t_s)$? Because when $N\to \infty$, Lyapunov spectrum approximates the probability distribution of eigenvalues of the Jacobian/Oseledets matrix?

aaab

Charlie Chang
  • 1,613

1 Answers1

1

A1:

$\delta$ indicates we integrate only over the set of $h=y^{-1}(y)$, i.e. $\int dh \delta(y-\phi'(h))\dots=\int_{h=y^{-1}(y)} dh\dots.$ Note that we use $\delta-$ function probably because we are dealing with a probability density function that is not monotonous.

$p(y)=\frac d{dy} P(h \le y^{-1}(y)) = p({h,-h})\frac d{dy} (y^{-1}(y)),$

where $p({h,-h})=2p(h)\\ y^{-1}(y) = ^+_- \sqrt{\mathrm{sech}^{-1}(y)}\\ \mathrm{sech}^{-1}(y)=\ln(\frac{1+\sqrt{1-y^2}}{y}).$

The steps that follows are not conducted, so not completely certain about details.

Overall, it is basic probability. For example, probability function of a function of random variables, there are two methods:

  1. $$ f_Z(z) = \int \delta\left(g(x_i)-z\right)f_{X_i}(x_i)dx_i, $$
    2. calculate:$$F_Z(z) = \int_{(x_1,\dots,x_n):g(x_1,\dots,x_n) \leq z} f_{X_1,\dots,X_n}(x_1,\dots,x_n) \ dx_1\cdots \ dx_n$$ and then$$f_Z(z) = \frac{d}{dz}F_Z(z).$$

A2:

$\chi(\lambda_i) = P(\lambda \le \lambda_i) = \frac{N+1-i}N$ for $\lambda_i$ is decreasing. Then $$\chi^{-1}\left(\frac{N+1-i}N\right) = \lambda_i.$$

Why the Oseledets $\Lambda$ instead of $D_{ij}(t_s)$? Perhaps because in this case $D_{ij}$ is constant ($J-I$). So $\Lambda=(T_t^T T_t)^{\frac 1 {2t}}=((D^t)^T (D^t))^{\frac 1 {2t}}=(D^T D)^{\frac12}$.

Why the real parts of eigenvalues of $D$? Possibly the singular values of a matrix are always real parts of the eigenvalues? (NOT sure.) For example, let $A=\left[ \begin{matrix} 1 & i \\ -i & i \end{matrix}\right].$

$D$'s eigenvalues follow the circular law.

Charlie Chang
  • 1,613