Representing graphs by an arrangement of chess rooks

Question

Consider a potentially infinite chessboard on which a number of rooks has been placed, under the restriction that any 2x2 square containing at least 3 rooks must contain a 4th rook.

This way, for every rook $x$ there is exactly one maximal rectangle of $n_x \times m_x$ rooks containing it. Furthermore, the relation of two rooks sharing the same maximal rectangle is an equivalence. Let us call those maximal rectangles vertices.

Two distinct vertices $A,B$ are said to share an edge if and only if there is a pair of rooks $x \in A, y \in B$ that can attack each other.

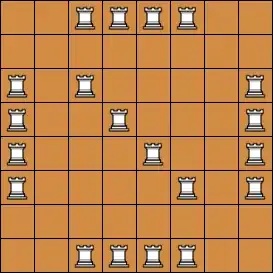
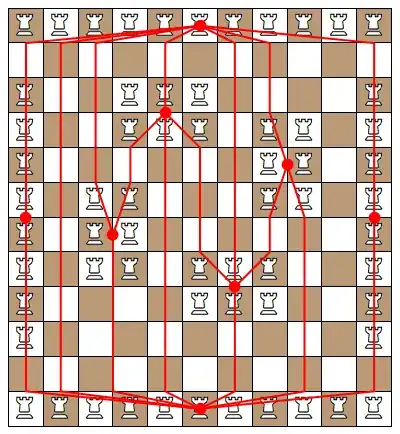
For instance, this arrangement of rooks forms the bull graph:

I wonder - are there simple graphs that cannot be represented in this manner?

I know that graphs of arbitrarily large genus can be represented, since it's trivial to create an arrangement representing the complete bipartite graph $K_{4,n}$ for any $n$ - and those have a genus of $\lceil \frac{n-2}2 \rceil$.

I haven't been able to contrive any way of representing the complete bipartite graph $K_{5,5}$, and I'm beginning to think those might be impossible. I also thought there might be no way of representing the complete graph $K_8$, but it turns out it can be done after all:

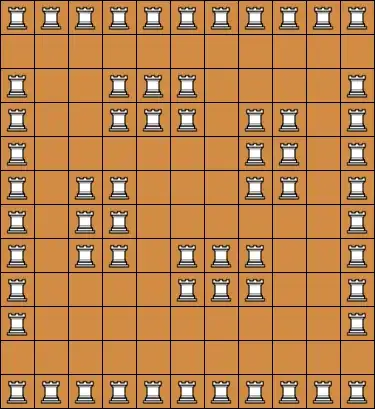Haven't tried to do $K_9$ yet.

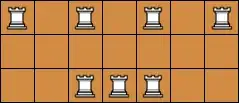
Here's a way to represent the complete bipartite graph $K_{4,4}$:

I don't know if this problem has been posed before or not, but I'm grateful for any help/references!

EDIT: my formulation of this problem has been inspired by the boardgame Meridians by Kanare Kato.

EDIT2: somehow managed to forget the word for "rectangle". English is not my first language, sorry!

EDIT 3: turns out $K_8$ can be done!

Answer 1

Yes, there are graphs that cannot be drawn in this way. I will give a partial characterization that proves in particular we cannot do $K_{11}$.

All graphs of this form can be decomposed into the edge union of two graphs:

• A "vertical graph" with an edge whenever two vertices $A,B$ contain a pair of rooks that can attack each other vertically;
• A "horizontal graph" with an edge whenever two vertices $A,B$ contain a pair of rooks that can attack each other horizontally.

Each of these can be drawn as a planar graph. Here is a picture of the "vertical graph" only for the diagram of $K_8$:

In general, here is how we embed the vertical graph as a planar graph. For each vertex $A$ (a rectangle of rooks) put a point in the geometric center of that rectangle. For each edge between $A$ and $B$, pick a vertical line where two rooks from $A$ and $B$ attack each other. Draw the edge that goes from the center of $A$, to the point on the boundary of $A$'s rectangle where the vertical line begins, to the point on the boundary of $B$'s rectangle where the vertical line ends, to the center of $B$.

These edges can't intersect inside the rectangles, because inside the rectangles we're just drawing straight lines from the center to the boundaries. They can't intersect outside the rectangles, because there we're just drawing vertical lines that (by definition of rooks attacking) don't pass through any other rectangles.

We can do the same thing for the horizontal graph. As a result, graphs that can be represented by rooks on a chessboard in this way are the union of two planar graphs. This imposes several restrictions, but in particular, if there are $n$ vertices, then each planar graph has at most $3n-6$ edges (for $n\ge 3$), so the union has at most $6n-12$ edges. Therefore $K_{11}$ is impossible, because it has $\binom{11}{2} = 55$ edges, which is more than $6\cdot 11 - 12 = 54$.

---

In the literature, these graphs appear to be known as rectangle visibility graphs. Not all unions of two planar graphs are rectangle visibility graphs; in particular, it seems that there is a slightly stronger upper bound of $6n-20$ edges in an $n$-vertex rectangle visibility graph (for $n\ge 5$). This proves that $K_8$ is the largest complete graph we can draw in this way: $K_9$ already has $36 > 6\cdot 9 - 20$ edges.

See, for example, the paper On representations of some thickness-two graphs by Hutchinson, Shermer, and Vince for more on rectangle visibility graphs.