I am reading "Principles of Mathematical Analysis 3rd Edition" by Walter Rudin.
What is $\alpha$?
I can imagine what $\beta(x)=\sum_{n=1}^{N} c_n I(x-s_n)$ is.
We can assume that $s_1<s_2<\dots<s_N$.
$\beta$ looks like the following picture:
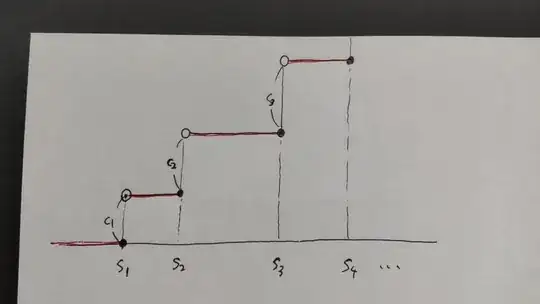
But when $N=\infty$, I cannot imagine what $\beta=\alpha$ is.
$\alpha$ can be continuous?
$\alpha$ can be differentiable?
6.14 Definition The unit step function $I$ is defined by $$I(x)=\begin{cases}0 & (x \leq 0),\\ 1 & (x > 0).\end{cases}$$
6.16 Theorem Suppose $c_n\geq 0$ for $n=1,2,3,\dots$, $\sum c_n$ converges, $\{s_n\}$ is a sequence of distinct points in $(a,b)$, and $$\alpha(x)=\sum_{n=1}^\infty c_n I(x-s_n).$$
Let $f$ be continuous on $[a,b]$. Then $$\int_{a}^{b}f\,d\alpha=\sum_{n=1}^\infty c_nf(s_n).$$