I assume knowledge of the Collatz conjecture. Here I'm looking only at total stopping times $t(n)$, and mostly will drop the word "total."
Just looking at relatively simple graphs of stopping times on Wikipedia shows many patterns in stopping times, sets of overlapping discontinuous "curves". In addition, if one zooms in closely, one finds pairs, triplets, or longer sequences of integers all with the same stopping time. This paper shows every pair of consecutive integers $(n, n+1) \equiv (4,5) \pmod 8$ have equal values of $t(n)$, other than the pair $(4,5)$.
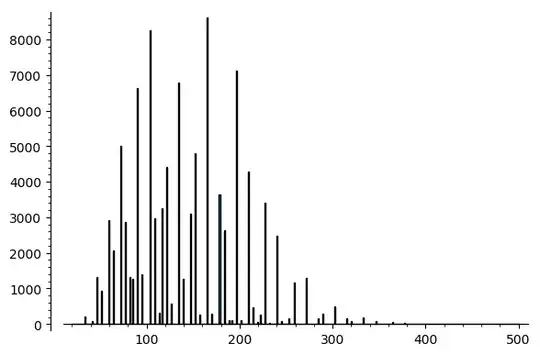
But this clustering extends over larger swaths of integers. Consider the integers in $[1000000,1100000]$. These $10^5$ integers have among them a total of just $69$ different stopping times, ranging from $20$ to $501$. Among those times, just $8$ of them account for over $50\%$ of the integers: $t = (72, 90, 103, 121, 134, 152, 165, 196)$. By contrast, $16$ of those $t$ values occur $10$ or fewer times, accounting for just $71$ of the integers in this range.
Within the range of values of $t$ taken, just $14\%$ are found, and just $1.66\%$ account for more than half the integers in the range. And as one looks at the same range sizes in larger integers, the clustering becomes more pronounced:
$$\begin{array}{c|c|c|c|c} \text{Range Start} & \text{Range of } t(n) & t \text{ values} & t \text{ values for 50%} \\ \hline 10^5 & [17, 382] & 167 & \sim40 \\ \hline 10^6 & [20, 501] & 69 & 8 \\ \hline 10^7 & [39, 618] & 48 & 5 \\ \hline 10^8 & [50, 686] & 40 & 4 \\ \hline 10^9 & [48, 803] & 34 & 4 \\ \end{array}$$
Now, obviously we shouldn't expect homogeneity of any sort. But this sort of clustering seems to be out of the realm of what we might expect. Over $20 \%$ of the integers $10^7 \leq n \leq 10^7 + 10^5$ all have the same total stopping time: $114$. They're not sequential, but that's a crazy statistic.
Does anyone know of an explanation--heuristic or otherwise--for this heavy clustering of the total stopping times?
The image below is a histogram of $t(n)$ values for $1000000 \leq n \leq 1100000$