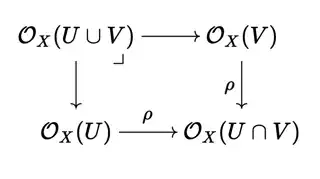Regular functions over the union of two principal open sets

Question

Been studying example 3.5 of Algebraic geometry and arithmetic curves by Qing Liu. Let $X = \operatorname{Spec} \mathbb Z[T]$. Let $p$ be a prime number. Then $(T, p)$ is a maximal ideal. Let $U \subset X$ denote the complement of the corresponding closed point. We have $U = D(p) \cup D(T)$. Therefore $O_{X}(U) \subset O_{X}(D(T)) \cap O_{X}(D(p))$. Not quite follow why this is true. First of all, where does this intersection even take place? My guess is they are all viewed as subspaces of the fraction field of $\mathbb Z[T]$. Then why would regular functions over the union be inside the intersection?

Answer 1

First, you're correct that this intersection is taking place in the fraction field of $\mathbb{Z}[T]$. Indeed, each $\mathcal O_X(V) = \left \{ \frac{f}{g} \ \middle | \ g(\mathfrak{p}) \neq 0 \text{ for each $\mathfrak{p} \in V$} \right \}$, so it's exactly the elements of the fraction field which satisfy some ~ bonus property ~ (that $g$ is nonvanishing on all the primes in $V$).

We know $\mathcal O_X(U)$ is the ring of all regular functions on $U = D(T) \cup D(p)$. That is,

$$ \mathcal O_X(U) = \left \{ \frac{f}{g} \ \middle | \ g(T) \neq 0 \text{ and } g(p) \neq 0 \right \} $$

This certainly looks like the intersection of $\mathcal O_X(T)$ and $\mathcal O_X(p)$ to me!

---

Edit:

When talking about algebraic geometry (particularly with people you don't know) it's hard to get the right level of abstraction for your audience. I try to lean concrete whenever possible, which is why I gave the example above (I'm also far from an expert in the more abstract approaches). In light of your comment, here's a more general way to go about this computation, which might be more helpful:

In general, $\mathcal{O}_X(U \cup V)$ is isomorphic to the pullback $\mathcal{O}_X(U) \times_{\mathcal{O}_X(V \cap U)} \mathcal{O}_X(V)$. That is:

where $\rho$ are the restriction maps. This is basically the gluing axiom, and depending on your experience, it might be helpful to work through that yourself.

If these $\rho$ are injective, then the projection from the pullback is also injective. This is because pullbacks preserve monos. Moreover, it's worth checking that the pullback of two injective maps is isomorphic to the intersection of the images of those maps (see here, for instance).

So as long as we can show these restriction maps are injective, then we'll know that $\mathcal{O}_X(U \cup V) \cong \text{"}\mathcal{O}_X(U) \cap \mathcal{O}_X(V)\text{"}$, where the scare quotes are because we're identifying these sets with their images in $\mathcal{O}_X(U \cap V)$.

Of course, in your case the restriction maps are injective, since they're just localization maps on an integral domain.

---

I hope this helps ^_^

Answer 2

The most explicit answer to your question is that $$\huge{\mathcal O_X(U)=\mathcal O_X(X)=\mathbb Z[T]}$$ Why? Because $X$ is a normal scheme and thus regular functions on $U$ extend uniquely to $X$, since the singleton closed set $X\setminus U$ has codimension $2$ in $X$.
This extension result follows from Theorem 1.14, Chapter 4, page 118 of Qing Liu's excellent book that you mention.
Can you see why this is compatible with HallaSurvivor's also correct answer?

PS I care for short-sighted people, as my displayed formula proves.