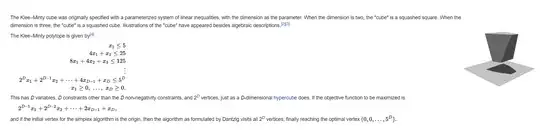
The Simplex Method pivoting rule that Victor Klee and George Minty used is the one that’s most used in practice: taking most positive improving column and using the minimum ratio test. But, because of this approach, others in the field have speculated that this rendition of the Simplex Algorithm only really considers local optimal solutions of each basis leading up to the global optimal basis, and in the worst case this could mean taking a long path to the global optimal solution because it doesn’t consider the global shape of the polytope. In other words, a large portion of reaching the global solution in the least amount pivots requires understanding how much the shape of the cube influences pivots. When improving pivots are done randomly in the Simplex Method, it is shown to take quadratically more pivots than it needs to on average. However, an interesting tangent is this: not only does the Simplex algorithm struggle with this cube, but also interior-point algorithms.
In practice, because a lot of abstracted problems are so specialized and well-defined that such theoretical issues like this one usually don’t occur.
A recent development using Fabio Vitor’s and Todd Eastman Double-Pivot Simplex Method on a few special cases of Klee-Minty cube found that it solved it in much better time than the original single-pivot variant by George Dantzig. Though, again this is due to the pivoting rule they chose for the Double-Pivot Simplex algorithm, further showing that the best-fitting pivoting rule for the problem matters.
Here is a review of the original Klee-Minty paper that summarizes it, and it’s impact, of the Klee-Minty cube.