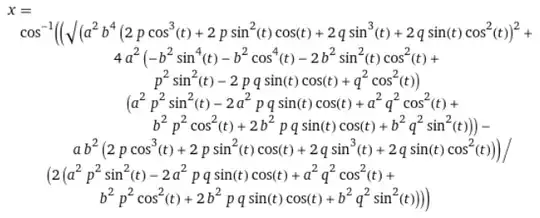Given an ellipse and a reference point, how to find the two lines that are tangent to the ellipse?

Question

I have an ellipse, possibly rotated and shifted from the origin, which is given by a parametrization similar to this one: $$ \begin{aligned} x &= x_0 + a\cos\theta\cos\alpha - b\sin\theta\sin\alpha \\ y &= y_0 + a\cos\theta\sin\alpha + b\sin\theta\cos\alpha \\ \end{aligned} $$

where $(x_0,y_0)$ is the center of the ellipse, $(a,b)$ are its semi-axes, $\alpha$ is the rotation angle and $\theta\in [0,2\pi]$.

The reference point is given by $(p_0,q_0)$. Now I want to determine the parameters of the lines $y = mx + h$ that are tangent to the ellipse and go through that reference point. To do so, I compute $h$ from the reference point, $h = q_0-mp_0$, and then plug the ellipse equations into the line equation: $$ \underbrace{y_0-q_0}_{\equiv q} + a\cos\theta\sin\alpha + b\sin\theta\cos\alpha = m\left(\underbrace{x_0-p_0}_{\equiv p} + a\cos\theta\cos\alpha - b\sin\theta\sin\alpha \right) $$ From this I can get an equation for the slope $m$ in dependence on $\theta$. I also know that the slope of a tangent to the ellipse is given by $\frac{y'(\theta)}{x'(\theta)}$, i.e.: $$ m = \frac{a\sin\theta\sin\alpha - b\cos\theta\cos\alpha}{a\sin\theta\cos\alpha + b\cos\theta\sin\alpha} $$

Now, if I equate the two above equations for $m$, I get an expression which can be solved for $\theta$. I would expect that there are two possible solutions to this equations, as there are two tangent lines. I used WolframAlpha to solve this equation (see here), but it gave me four different solutions (which differ in the combination of two signs); I'm including a screenshot of one of the solutions below since it's quite long ($x\equiv\theta, t\equiv\alpha$):

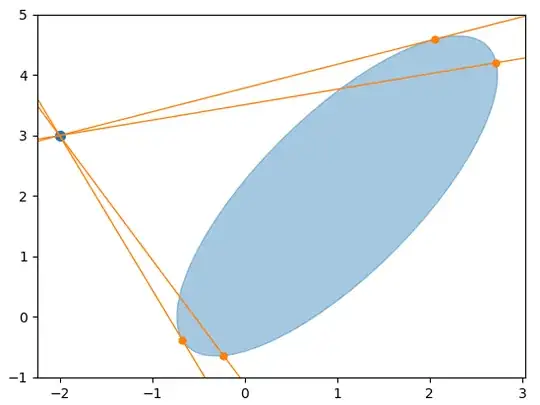
The four solutions emerge as $x = \pm\cos^{-1}((\pm\sqrt{\dots}$. There are no additional constraints mentioned, so something must have gone wrong, but I can't figure out what. I verified that two of those four solutions are valid with the help of some examples (testing various reference points p0,q0):

import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
import numpy as np
from numpy import arccos, cos, pi, sign, sin, sqrt
a, b = 3, 1  # ellipse parameters
center = 1, 2  # center of ellipse
angle = 60  # rotation of ellipse (counter-clockwise) [deg]
p0, q0 = -2, 3  # the reference point (x-,y-coordinates)
p = center[0] - p0
q = center[1] - q0
t = angle/180pi
thetas = [
    s1arccos((s2sqrt(a2b4(2p*cos(t)3 + 2psin(t)2cos(t) + 2q*sin(t)3 + 2qsin(t)cos(t)2)2 + 4a2*(-b2sin(t)4 - b2cos(t)4 - 2*b2sin(t)2cos(t)2 + p2sin(t)2 - 2pqsin(t)cos(t) + q2cos(t)2)*(a2p2sin(t)2 - 2*a2pqsin(t)cos(t) + a2*q2cos(t)2 + b2p2*cos(t)2 + 2b2pqsin(t)cos(t) + b2q2*sin(t)2)) - ab2(2pcos(t)3 + 2psin(t)2cos(t) + 2qsin(t)3 + 2qsin(t)cos(t)2))/(2*(a2p2sin(t)2 - 2*a2pqsin(t)cos(t) + a2*q2cos(t)2 + b2p2*cos(t)2 + 2b2pqsin(t)cos(t) + b2q2*sin(t)2)))
    for s1 in [-1, 1] for s2 in [-1, 1]
]
fig, ax = plt.subplots()
ax.add_patch(Ellipse(center, 2a, 2b, angle, color='tab:blue', alpha=0.4))
ax.scatter([p0], [q0], color='tab:blue', s=50)
for theta in thetas:
    ex = center[0] + acos(theta)cos(t) - bsin(theta)sin(t)
    ey = center[1] + acos(theta)sin(t) + bsin(theta)cos(t)
    ax.axline((p0,q0), (ex,ey), color='tab:orange', lw=1)
    ax.scatter([ex], [ey], color='tab:orange', s=25)
plt.show()

So it seems that all that's left is to find a way how to pick the right combinations of signs for the two tangent points. However, I don't know what condition I should apply. I tried to discriminate based on the quadrant of $(p_0-x_0,q_0-y_0)$, but that didn't work. Also, since there are 6 different ways to pick 2 out of 4 possible sign combinations, it seems that the condition should include 6 different "sections/intervals".

Answer 1

There can be only two solutions.

You can make the problem much simpler by transforming the ellipse to a circle (rotate by $-\alpha$ and stretch by $(\frac1a,\frac1b)$), and move it to the origin. Apply the same transformation to the external point.

Now you can solve by simple trigonometry or express that the point of contact defines a right angle:

$$(p-\cos t)\cos t+(q-\sin t)\sin t=0$$

or $$\cos\left(t-\arctan\frac qp\right)=\frac1{\sqrt{p^2+q^2}}.$$

Answer 2

One way is to use the equation which is $$(\frac{(x-x_0)\cos(\alpha)+(y-y_0)\sin(\alpha)}{a})^2+(\frac{-(x-x_0)\sin(\alpha)+(y-y_0)\cos(\alpha)}{b})^2-1=0.$$

Then the equation of the line pair (tangents from $(p_0,q_0)$) are by joachimsthal $s\cdot s_{11}-s_1^2=0$ or

$((\frac{(x-x_0)\cos(\alpha)+(y-y_0)\sin(\alpha)}{a})^2+(\frac{-(x-x_0)\sin(\alpha)+(y-y_0)\cos(\alpha)}{b})^2-1)((\frac{(p_0-x_0)\cos(\alpha)+(q_0-y_0)\sin(\alpha)}{a})^2+(\frac{-(p_0-x_0)\sin(\alpha)+(q_0-y_0)\cos(\alpha)}{b})^2-1)\\-((\sin(\alpha)^2/b^2+\cos(\alpha)^2/a^2)xp_0+((\cos(\alpha)\sin(\alpha))/a^2-(\cos(\alpha)\sin(\alpha))/b^2)(xq_0+p_0y)+(\cos(\alpha)^2/b^2+\sin(\alpha)^2/a^2)yq_0+((\cos(\alpha)\sin(\alpha)y_0)/b^2-(\cos(\alpha)\sin(\alpha)y_0)/a^2-(\sin(\alpha)^2x_0)/b^2-(\cos(\alpha)^2x_0)/a^2)(x+p_0)+((-(\cos(\alpha)^2y_0)/b^2)-(\sin(\alpha)^2y_0)/a^2+(\cos(\alpha)\sin(\alpha)x_0)/b^2-(\cos(\alpha)\sin(\alpha)x_0)/a^2)(y+q_0)+((\cos(\alpha)^2y_0^2)/b^2+(\sin(\alpha)^2y_0^2)/a^2-(2\cos(\alpha)\sin(\alpha)x_0y_0)/b^2+(2\cos(\alpha)\sin(\alpha)x_0y_0)/a^2+(\sin(\alpha)^2x_0^2)/b^2+(\cos(\alpha)^2x_0^2)/a^2-1))^2=0$

which simplifies to

$$\frac{((y_0-q_0)^2-((b^2-a^2)\cos(2α)+a^2+b^2)/2)(x-p_0)^2+(\sin(2α)(a^2-b^2)-2(x_0-p_0)(y_0-q_0))(x-p_0)(y-q_0)+((x_0-p_0)^2+((b^2-a^2)\cos(2α)-(a^2+b^2))/2)(y-q_0)^2}{a^2b^2}=0$$ which you can factor by setting $t=\frac{x-p_0}{y-q_0}$ (or its inverse) and using the quadratic formula to get

$$(x-p_0)-(y-q_0)\frac{2(x_0-p_0)(y_0-q_0)+\sin(2α)(b^2-a^2)\pm\sqrt{D}}{2(y_0-q_0)^2-((b^2-a^2)\cos(2α)+b^2+a^2)}=0$$

where

$$D=2(a^2+b^2+(a^2-b^2)\cos(2\alpha))(y_0-q_0)^2 +4(b^2-a^2)\sin(2\alpha)(x_0-p_0)(y_0-q_0) +2((b^2-a^2)\cos(2\alpha)+b^2+a^2)(x_0-p_0)^2-4a^2b^2$$

Answer 3

Let $x=x_0+a\cos\theta\cos\alpha-b\sin\theta\sin\alpha$, $y=y_0+a\cos\theta\sin\alpha+b\sin\theta\cos\alpha$ is ellipse point with parameter $\theta\in[0;2\pi)$. Then slope of line going through this point and reference point $(p_0,q_0)$ is $$k=\frac{y-q_0}{x-p_0}=\frac{y_0-q_0+a\cos\theta\sin\alpha+b\sin\theta\cos\alpha}{x_0-p_0+a\cos\theta\cos\alpha-b\sin\theta\sin\alpha}=\frac{A+B\cos\theta+C\sin\theta}{D+E\cos\theta+F\sin\theta}$$

$$\frac{dk}{d\theta}=\frac{CE-BF+(CD-AF)\cos\theta+(AE-BD)\sin\theta}{(D+E\cos\theta+F\sin\theta)^2}.$$

Tangent points will be determined by $$CE-BF+(CD-AF)\cos\theta+(AE-BD)\sin\theta=0$$ $$\frac{(CD-AF)\cos\theta+(AE-BD)\sin\theta}{\sqrt{(CD-AF)^2+(AE-BD)^2}}=\frac{BF-CE}{\sqrt{(CD-AF)^2+(AE-BD)^2}}$$ $$\cos\beta=\frac{AE-BD}{\sqrt{(CD-AF)^2+(AE-BD)^2}},\; \sin\beta=\frac{CD-AF}{\sqrt{(CD-AF)^2+(AE-BD)^2}}$$ $$\sin(\theta+\beta)=\frac{BF-CE}{\sqrt{(CD-AF)^2+(AE-BD)^2}}$$ $$\theta_1=-\beta+\arcsin\frac{BF-CE}{\sqrt{(CD-AF)^2+(AE-BD)^2}},$$ $$\theta_2=\pi-\beta-\arcsin\frac{BF-CE}{\sqrt{(CD-AF)^2+(AE-BD)^2}}$$

The calculation procedure: given $x_0$, $y_0$, $a$, $b$, $\alpha$, $p_0$, $q_0$. Calculate $A$, $B$, $C$, $D$, $E$, $F$. Then calculate $\cos\beta$, $\sin\beta$, $\sin(\theta+\beta)$ by formulae from above. Then find $\beta$ and two values of $\theta$. Then calculate $(x,y)$ for both tangent points, using $\theta_1$ and $\theta_2$.

Answer 4

Your given ellipse is of the form

$ p(t) = C + V u $

where

$ V = [v_1, v_2] , u = [\cos t , \sin t ]^T $

Here, $v_1 = \begin{bmatrix} a \cos \theta \\ a \sin \theta \end{bmatrix} \hspace{10pt} v_2 = \begin{bmatrix} - b \sin \theta \\ b \cos \theta \end{bmatrix} $

$\theta$ is the rotation angle of the ellipse, and $t$ is the parameter.

Note that

$ V = R D $

where

$ R = \begin{bmatrix} \cos \theta && - \sin \theta \\ \sin \theta && \cos \theta \end{bmatrix} \hspace{10pt} D = \begin{bmatrix} a && 0 \\ 0 && b \end{bmatrix} $

Consider the transformation matrix

$ A = D^{-1} R^T $

Apply this to the point $p$, you get

$ p' = A p = D^{-1} R^T C + u $

So that $p'$ lies on a circle with center at $ C' = D^{-1} R^T C $. Apply the same transformation to the reference point $P = (p_0, q_0) $, you get its image given by

$ Q = A P = D^{-1} R^T P $

Note that the linear transformation $A$ preserves the tangency between the original ellipse, and its transformed image which is the unit circle centered at $C'$.

Let $d$ be the distance between $Q$ and $C'$, then

$ d = \| D^{-1} R^T P - D^{-1} R^T C \| = \| D^{-1} R^T (P - C) \| $

We want to draw two tangents from $Q$ to the unit circle centered at $C'$. So define the angle

$ \phi = \sin^{-1} \left( \dfrac{1}{d} \right) $

Then $\phi$ is the angular displacement of the two tangents from the line connecting $Q$ and $C'$. Define the vector $V = C' - Q = (V_x, V_y)$, and let $\alpha$ be the angle this vector makes with the positive $x$ axis, then

$ \alpha = atan2(V_x, V_y) $

where $atan2(x_1, x_2)$ returns the angle $\psi$ such that

$ \cos \psi =\dfrac{x_1}{\sqrt{x_1^2+x_2^2}}$ and $\sin \psi = \dfrac{x_2}{\sqrt{x_1^2+x_2^2} }$

And let $ m = tan(\alpha) $

The slopes of the two tangents are easy to calculate, let their angles be $\beta_1 $ and $\beta_2$ , then

$ \beta_1 = \alpha + \phi $ , $ \beta_2 = \alpha - \phi $

Therefore, the slopes are

$ m_1 = \tan(\beta_1) = \dfrac{ m + f }{1 - m f} \hspace{10pt} $

$ m_2 = \tan(\beta_2) = \dfrac{ m - f}{1 + m f} $

where $ f = \tan(\phi) $

We have a common point on the two tangents which is $Q$ and their slopes $m_1$ and $m_2$. If $Q = (q_1, q_2)$ then the equation of the first tangent is

$ y = q_2 + m_1 (x - q_1) $

And the equation of the second tangent is

$ y = q_2 + m_2 (x - q_1) $

These two equations can be written in vector form as

$ n_1^T (r' - Q) = 0 $

and

$ n_2^T (r' - Q) = 0 $

where $ r' = (x, y) $ and $ n_1 = [m_1, -1], n_2 = [m_2, -1] $ are the normal vectors to the two tangents.

Finally, recall that $ r' = A r = D^{-1} R^T r $. Therefore, the equations of the two tangents to the ellipse are

$ n_1^T ( D^{-1} R^T r - Q ) = 0 $

and

$n_2^T (D^{-1} R^T r - Q ) = 0 $

But $Q = D^{-1} R^T P $

Hence, the equations of the two tangents can be written as

$ ( R D^{-1} n_1 )^T (r - P) = 0 $

And

$ ( R D^{-1} n_2 )^T (r - P) = 0 $

---

Appendix:

The two tangency point for the unit circle are given by

$ T'_1 = C' + [\cos(\alpha + \pi - ( \dfrac{\pi}{2} - \phi) ) , \sin (\alpha + \pi - ( \dfrac{\pi}{2} - \phi ) ) ] $

$T'_2 = C' + [ \cos(\alpha + \pi + ( \dfrac{\pi}{2} - \phi) ), \sin (\alpha + \pi + (\dfrac{\pi}{2} - \phi) ) ] $

These two expressions simplify to

$ T'_1 = C' + [ - \sin( \alpha + \phi ) , \cos (\alpha + \phi ) ] $

$ T'_2 = C' + [ \sin ( \alpha - \phi) , - \cos (\alpha - \phi) ] $

The corresponding tangency point in the original space (before transformation) are

$ T_1 = A^{-1} T'_1 = R D T'_1 $

$ T_2 = A^{-1} T'_2 = R D T'_2 $

The figure below shows an example that uses the formulas developed above, for an ellipse with semi-major axis of $a = 5$ and semi-minor axis of $b = 2$, and an angle of inclination of $\theta = 45^\circ$. The center is at $C = (3, -1)$ and the reference points is $P = (12, -3) $. The two tangent lines and the tangency points are shown.