Simply put, are most functions in the "real world" non-convex?

Question

Is it "safe" to say that natural phenomena in the real world are often characterized and modelled by functions exhibiting irregular and complicated behaviors, and such functions are almost never convex?

Just as an example, if we take the functional form of the "loss functions" that are optimized in Neural Networks (popular class of Machine Learning Algorithms) - these "loss functions" are often multidimensional and are said to have highly complicated and irregular shapes and forms. Below are some visualizations of the "loss functions" from a Convolutional Neural Network (CNN), used in image recognition:

I have heard people make such claims, such as the "loss functions" of real-world Neural Networks are often so complicated that it is almost "pointless" to write them out in "implicit function form" (e.g. f(x,y,z) ). This being said, given their complexity and the bulk of research that is specifically being conducted regarding the "convergence of optimization algorithms (such as gradient descent) on non-convex functions" - is it "safe" to say that such types of "loss functions" from Neural Networks are almost never convex?

Thanks!

References:

• https://jithinjk.github.io/blog/nn_loss_visualized.md.html

EDIT Note: Take the classic forms of loss functions for Neural Networks:

Is it possible to tell in general if these functions are convex or non-convex?

Answer 1

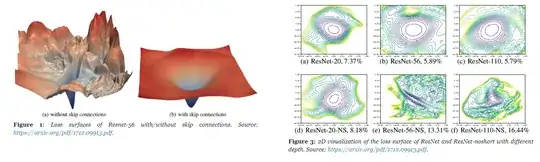
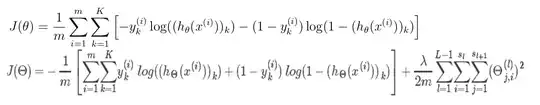When researchers say something as inflammatory and unscientific as "Most Functions in the 'Real World' are Non-Convex", they are pushing back against the shared assumptions of a research field, not trying to make a rigorous statement.

In this case, the speaker is making a statement about convexity in optimization. To understand the speaker's perspective it helps to understand the history of research in mathematical programming/optimization. This additional context allows one to interpret the speaker's claim for what it is; a critique of current research culture.

The foundation of mathematical programming is linear programming, introduced alongside the simplex method of George Dantzig for solving such problems in the 1940s and 50s. It's not a coincidence that these dates overlap with World War 2. George Dantzig was solving Operations Research problems for the US Armed Forces when he made these contributions. The simplex method was a very big deal, but it had its weaknesses as well. In particular, there are certain problems for which the simplex method requires an exponential number of operations as a function of its input dimensions (see the Klee-Minty cube).

However, linear programs are in fact polynomially time solvable, and in the late 1980 and 1990s there was revised interest in alternative methods which attain these bounds, such as the ellipsoid method. Interior point methods, which are an alternative method for solving linear programs, also became a very hot topic. People realized that interior point methods can be fairly easily extended to any conic program (a class of optimization problems slightly more restricted than the more general convex programs). From this point until the 2010s optimizers focused almost exclusively on convex optimization problems. The theory of convex optimization is very attractive from a theoretical point of view, so there was a strong desire to stay within this class of problems as often as possible. As an example which you are likely already aware, neural networks were viewed as inferior to support vector machines for a long time. The fact that fitting a support vector machine is a convex optimization problem was likely a major reason why. But In 2012 there was an important breakthrough that began to change the optimization landscape; the neural network AlexNet, the fitting of which is nonconvex, won ILSVRC 2012 (aka imagenet). This kicked off a flurry of research activity on variants of stochastic gradient descent, the primary method used for fitting neural networks.

The speaker is now suggesting that optimizers need to move more firmly beyond the neat and tidy theory of convex optimization, because there are important problems that fall outside of this class (like fitting neural nets or matrix completion models). But research fields have inertia, and it's difficult for a speaker to get an entire research community to move beyond the convexity that they likely studied in their PhD theses. Hence the speaker resorted to something inflammatory, attention-grabbing, and unverifiable. The speaker did this as a way to get people talking and thinking about their claims. The existence of this question suggests that he/she has at least partially succeeded.

My opinion is that there are important problems to solve in both convex and nonconvex optimization. I don't fault researchers for using a theoretically attractive class of problems as often as they can. I also don't think the speaker's assertion is particularly novel or insightful anymore, since at this point AlexNet's revolutionary success was a decade ago.

Answer 2

I can’t speak for ML stuff as I’m no expert on it, and it’s generally a marginal subject compared to the vast amount of nonlinear problems arising in all other disciplines.

In my experience, in many real life problems you can’t even write down your objective function(s): in quite a few cases, their value may be the result of extremely complex numerical simulations coming from black boxes, proprietary tools. Which may take hours or days per function evaluation. And those functions can be horrendous (even in a very low dimensional problem), multimodal (with thousands of local minima/maxima). Sometimes they can be discontinuous, or non differentiable.

There has to be a reason why gradient descent is so popular in the ML disciplines. Maybe for some obscure miracles it works acceptably well for ML problems. This is definitely not the case in any other problem I’ve ever encountered in other disciplines: gradient descent is possibly the worst optimization algorithm you can think of when optimizing a nonlinear function.

Unless of course “gradient descent” has a different meaning in the ML world compared to the textbook definition of it.