I'm taking Brilliant.org's calculus course, and I'm on the section called The Derivative.
My (mis)understanding:
A tangent line is a linear function that grazes a point, $a$, on the graph of a different function. The slope of that tangent line is the instantaneous rate of change at $a$. The way you find this is by taking the difference ratio, giving you the slope, and plugging in equal values for the input points. So, for the function $f(x) = x^2$, the slope would be:
$$\require{cancel} \frac{b^2 - a^2}{b-a} = \frac{\cancel{(b-a)}(b+a)}{\cancel{b-a}} = b+a$$
Now, considering the case as the difference between $b$ and $a$ gets smaller, or equivalently, as the secant line's two points become one and the same point, thus turning it to a tangent line:
$$\lim_{b \rightarrow a} b +a = 2b = 2a$$
Thus, the derivative of the square function is found, $f'(x) = 2x$. The slope of the tangent is $2x$, but apparently, the derivative isn't the slope of the tangent, it is only so the other way around (see this Math.SE answer). I could define any number of functions of the form $g(x) = ax$, which would be tangent to or intersect the function $f(x)=x^2$, when $x=a$. For any of these functions, $g'(x) = a$, as per the difference ratio. The slopes of these functions would be any arbitrary number $a$, not $2x$. So, it seems we're dealing with the slope of one particular tangent. However, I can't see how this tangent line is linear. If it is linear, its slope is a constant, but $2x$ contains a variable.
All of this leads me to think that we're talking about the tangent line in a very different sense than the one of "a linear line that grazes the function's graph". But I've only been made familiar with the latter sense, and this mysterious sense is very ill-defined in my head. What is it and what does it have to do with tangent lines? The trick with morphing a secant line into a tangent line doesn't really explain this, because one can do that anywhere on the graph and wind up with tangent lines that have differing slopes, none of which are equal to $2x$.
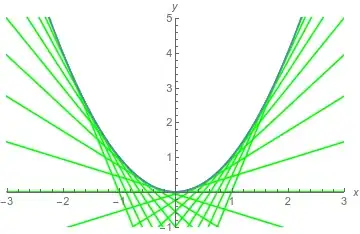
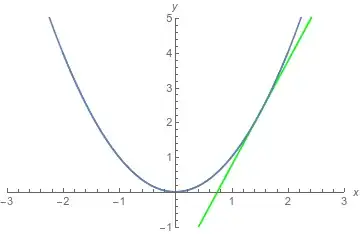

$$\begin{align} \frac{y - f(3)}{x-3} &= f'(3)\ y &= 6(x-3)+9 \end{align}$$
(This is a straight line on the $xy$-plane)
– peterwhy Jan 03 '22 at 02:30