2

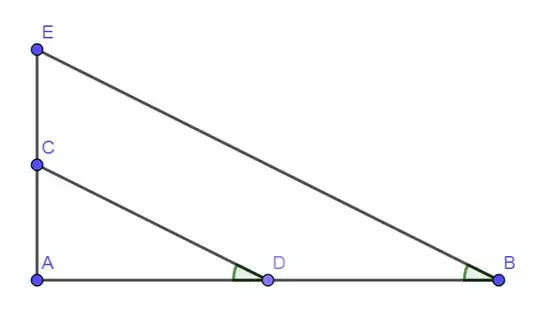
Suppose that $a,b > 1$ are real numbers. Consider the following picture, enter image description here

Where $AD = 1$, $AB = a$, $AC = b$, and $\angle ADC = \angle ABE$.

We can define, the product $a\cdot b$, geometrically as the length of $AE$.

I was able to prove geometrically that $(ab)c = a(bc)$. However, how does one justify the commutative law $ab=ba$?

Usually we think of $ab$ as representing the area of a rectangle and so the area does not change when the rectangle is rotated sideways. However, I am curious how we do this if we stick to proportions only.

Nicolas Bourbaki
  • 5,553
  • Use the properties of proportions: $$1:a=b:AE\implies 1:b=a:AE.$$ – Intelligenti pauca Dec 29 '21 at 09:19
  • I think I got the answer. Let me know if the following thought answer your question precisely. Since angle $ADC=ABE$, $\frac{b}{1}=\frac{AE}{a}$. So $(AE)\cdot 1= AE = a\cdot b$. Because sum of the triangle is 180, angle $ACD=AEB$. Now look at your diagram from $AE$ base or rotate your triangle by 90 degree so that $AE$ goes to X axis and $AB$ goes to Y axis. So that $\frac{AE}{a}=\frac{b}{1}$, $AE= b\cdot a$. Thus $AE= b\cdot a= a\cdot b$. – user264745 Dec 29 '21 at 09:20
  • Otherwise, you can use Pascal's Theorem and avoid proportions altogether. You can find the details in Hilbert's "The foundations of geometry", §15 in 1950 reprint. – Intelligenti pauca Dec 29 '21 at 09:32
  • @Intelligentipauca My "issue" with your first comment is that my motivation is to think of $\mathbb{R}$ geometrically, and think of $+$ and $\cdot$ as representing certain lengths. The argument feels very circular (not that it is wrong). – Nicolas Bourbaki Dec 29 '21 at 09:38
  • 1
    @user264745 Unfortunately, this is not what I am looking for. I am deliberately trying to avoid thinking of "numbers", and only think of "lengths", therefore writing $\frac{AE}{a}$, does not make sense here. (In actuality, what you write is correct, but I am intentionally trying to avoid using numbers and use congruence instead.) – Nicolas Bourbaki Dec 29 '21 at 09:40
  • @NicolasBourbaki You are right, because the classic (Euclid's) definition of proportion requires the notion of integer multiple. Not circular, but probably not what you are looking for. Go with Hilbert, then. – Intelligenti pauca Dec 29 '21 at 09:41
  • @Intelligentipauca When you say to look at Hilbert, are you saying that Hilbert proves this result by congruence in his book? – Nicolas Bourbaki Dec 29 '21 at 09:43
  • Yes, he does. And that book is not difficult to find online. – Intelligenti pauca Dec 29 '21 at 09:45
  • See this thread. The key to commutativity in affine and projective planes is the Pappus theorem. I would echo the recommendation in that thread of John Stillwell’s The Four Pillars of Geometry. – Mo Pol Bol Dec 30 '21 at 13:56

1 Answers1

1

In the following diagram: 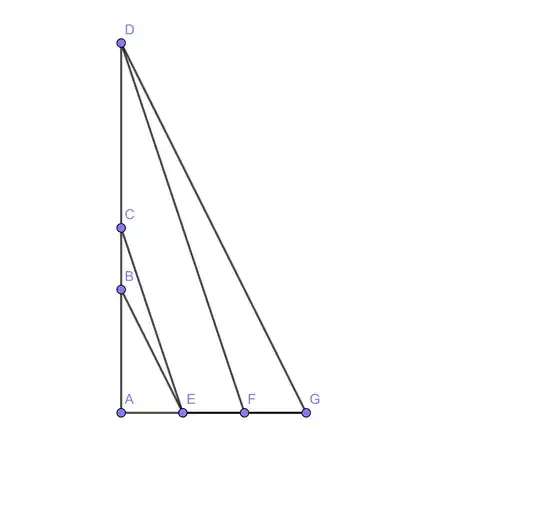enter image description here

  • $\overline{AE}$ is of length $1$.
  • $\overline{AF}$ is of length $b$.
  • $\overline{AG}$ and $\overline{AC}$ are of length $a$.
  • $\angle BEA=\angle DGA$.
  • $\angle CEA = \angle DFA$.

It is sufficient to demonstrate that $\overline{AB}$ is congruent to $\overline{AF}$.

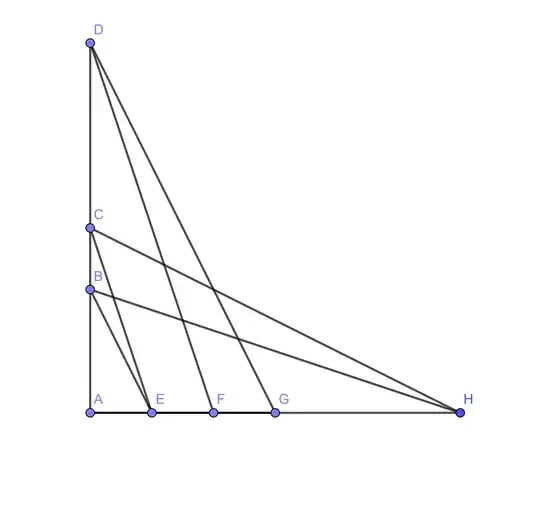
Extend segment $\overline{AG}$ to point $H$ such that segment $\overline{AH}$ is congruent to segment $\overline{AD}$. Additionally, segments $\overline{CH}$ and $\overline{BH}$ are constructed. enter image description here

Now, observe that $\triangle ADG$ is congruent to $\triangle AHC$ by SAS. Due to this $\angle ACH= \angle AGD$.

By construction, $\angle AGD=\angle AEB$. Therefore, $\angle ACH=\angle AEB$.

As a result, $\angle BEH$ is the supplementary angle of $\angle ACH$, and so the quadrilateral $EBCH$ has opposite angles that are supplementary, meaning it is a cyclic quadrilateral, then $\angle CHB= \angle BEC$.

We have $\angle BEC =\angle AEC - \angle AEB$. So $\angle CHB = \angle AEC - \angle AEB$.

By the exterior angle theorem, $\angle ABH =\angle CHB + \angle BCH = (\angle AEC - \angle AEB) + \angle ACH = \angle AEC - \angle AEB + \angle AEB = \angle AEC$.

Finally, by AAS criterion, $\triangle AFD$ is congruent $\triangle ABH$. Therefore, segment $\overline{AB}$ is congruent to segment $\overline{AF}$.

Cris
  • 320