4

I need help with the relationship between the variables and the derivatives

In the below question, I thought it would be something like $\tan(\theta)=\frac{y}{x}$ where $y=40t$ and $x=25-30t$. And then, at the maximum, there would be no change in the angle so it would be zero. But when I differentiate, I get $0=\frac{40(25-30x)+30(40x)}{(25-30x)^2}$

If my intuition is correct, I'd want to say that the distance is closest when it's an isosceles triangle - that is, when $x=y$ and so I could find some other values.

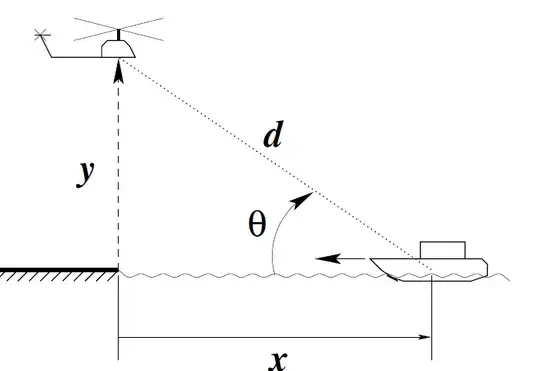
enter image description here

A navy vessel is located at $25$ km from the enemy shoreline where an enemy helicopter base is located. The vessel is moving toward the base at a constant speed of $v_p = 30$ km/h. At this time (referred to as $t = 0$ for convenience), its early warning radar detected that an enemy helicopter is located on the ground in the base and is taking off vertically with a constant speed $v_h = 40$ km/h (see figure). To determine the optimal time to fire a laser beam to shoot down the helicopter, the following information must be provided to the commander.

(a) At what time will the distance between the vessel and the helicopter be shortest? What is this distance? Assume that the speeds and directions of both the vessel and helicopter are constant.

(b) The laser is kept pointing directly at the helicopter at all times. At the time found in (a), what is the rate of change of the angle theta at which the laser is aimed (see figure)?

bjcolby15
  • 4,210
Ally
  • 117
  • 1
    You've got $x(t)$ and $y(t)$ correct. You want to know when the distance $d$ is shortest, which means you want to minimize $d$ with respect to $t$. So, first, you need to figure out what $d$ is as a function of $t$. If you can get the relationship between $x$, $y$, and $d$, you can substitute in the expressions you found for $x(t)$ and $y(t)$, and differentiate from there. – Amaan M Dec 15 '21 at 03:59
  • You'll want to use $\tan \theta = y/x$ for the second question, but to find the time when $d$ is minimized, you don't need it. For the second one, don't forget to use the chain rule on the left hand side, when you differentiate $\tan \theta$, you should get $\sec ^2 (\theta) \cdot \frac{d\theta}{dt}$. – Amaan M Dec 15 '21 at 04:03
  • 1
    Thanks, so the first question is actually a Pythagorean theorem question (I suppose it's the $\theta$ in the picture that misled me into thinking it was some sort of ratio) Because now I got $t=3/10$ and that makes the second part easy since I know various $x$ and $y$ values to substitute into the quotient rule on the right side and the chain rule on the left. – Ally Dec 15 '21 at 04:28
  • Why would you expect the angle to be stationary ever? If the helicopter is stationary, the approaching boat causes $\theta$ to increase. If the boat is stationary, the rising helicopter causes $\theta$ to increase. Together, we know that $\theta(t)$ is a strictly monotonically increasing function, so its derivative is never zero. – Eric Towers Dec 15 '21 at 05:35

0 Answers0