0

The question is in the title itself.

How to calculate the number of possible connected simple graphs with $n$ labelled vertices

This is much like the above posted link except that it is more complicated because now not only the graphs are labelled but the label can change among themselves. For example if in a graph with 4 vertices, cyclically the vertices are 1,2,3 and 4. Then some configuration may involve 1,3,2 and 4 cyclically. This is not the same as unlabeled case. I don't know the correct terminology for those graphs "whose labels can permute among themselves".

For example--- enter image description here

So for 2 vertex simple connected graph we have the number of possibilities as 1, for 3 vertex graph it is again 1, for 4 vertex graph it becomes 10. What is the general form(if there is any)?

This is precisely the value of number of possible $l$ clusters used in cluster expansion in statistical mechanics.

Manas Dogra
  • 354
  • So there is also restriction that the graphs have at least a cycle through all the vertices? – gilleain Dec 05 '21 at 20:15
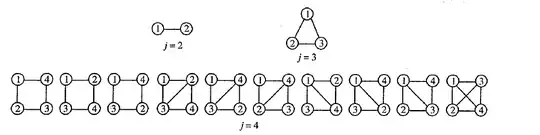
  • I do not understand why you include 1 --- 2 for 2-vertex graphs but not the path graph 1 --- 2 --- 3 --- 4 for 4-vertex graphs. If it weren't for the 2-vertex case, I would think that what you're counting is the number of labeled graphs with a Hamiltonian cycle. – Misha Lavrov Dec 05 '21 at 21:03

0 Answers0