4

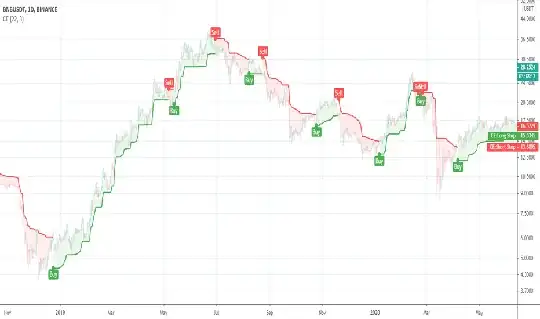
given an initial 1000 dollars cash value, and a time series of bid price, ask price, assuming constraints of transaction costs, e.g. 1 dollar every time we buy or sell, what is the best approach to finding buy and sell points that maximize the profit generated by a trading algorithm? (i.e. buy low sell high and/or sell high buy low)

just to be clear, not trying to predict anything here, just looking back at past prices, and trying to figure out what would have been the best course of action given transaction costs constraints

example of buy/sell points we want to identify

I am thinking of making this a classification problem, with decisions being either of buy/sell/donothing, or an optimization problem, with each variable being a point in time, assigning +1/-1 weight to each, or simply calculating the derivative of the price curve and each time it is zero (changing direction/reverting), then taking position but I am not sure how to have constraints in there, or maybe have a lookback window of the past 100 points, and find the optimal path

John
  • 103
  • there are similar questions out there, but I have a hard time figuring out which constrains/how to formulate this problem into a linear optimization one – John Nov 26 '21 at 05:11
  • I think is not possible to follow your idea because of two issues: knowing when to come in and out is similar to the halting problem which is not solvable, and also it will make you millionaire going against the principle of the Fundamental theorem of asset pricing, but also, prices are modeled as Brownian paths with finite quadratic variation, so they are nowhere differentiable (think of them as it were a continuous function made of discrete jumps in every point). – Joako Nov 28 '21 at 15:09
  • thanks for the input, but it clearly is possible to find the mins and max given entry and exit costs constraints, I can do it manually, if the constraint is big enough, it will just the min and the max of the window, so there is definitely a way to define this mathematically; nothing to do with being a millionaire or asset pricing, just looking at a time series snapshot and trying to find local mins and max, it is at worse a linear optimization problem, and at best hopefully an nlog(n) complexity algo – John Nov 29 '21 at 14:45
  • might even be a linear time complexity algo, I suspect it is some variant of the "largest rectangle in a histogram" problem, see https://www.geeksforgeeks.org/largest-rectangular-area-in-a-histogram-set-1/ – John Nov 29 '21 at 15:30
  • Just to make one thing clear: you want to end with pure cash asset at the end without any stock positions, right? – fedja Nov 29 '21 at 23:23
  • thanks, valid question, I am pretty agnostic to that, the point being to identify lows and highs, so you can buy first and sell after, or sell first and buy after, or simply buy at the lowest, and keep an open position, whatever makes the problem simpler to resolve. If making the assumption that we end up with cash helps, then feel free to simplify the problem. – John Dec 02 '21 at 01:03
  • @John in my first comment I say it so because of I believe it can´t be defined what "optimal" will means: if a specific time $t_0$ I made a buy/sell decision, following some analysis bases on past data information $Info(t<t_0)$, after have passed a period of time $T$, I could be saying it was good or bad if at time $t_0+T$ I have more money, but it actually since at time $t_0$ the information $Info(t_0<t<t_0+T)$ was nonexistent, and just because of randomness it could happen many other different paths which some could have made you loose money instead of winning..., – Joako Dec 03 '21 at 00:27
  • @John It would be "fair" to decide as optimal the final occurring path where the decision was made with just the information at $Info(t<t_0)$?? and equivalently it extends to all time $t$... so How you will be defining the decisions are being optimal or not? Through the finally occurring path? Comparing against the mean value of your projections at $Info(t<t_0)$?... So some "fair" definition of what is "optimal" is needed, and here is were I believe you will crash with the "Halting problem" issues: I have won because of a good decision or just because of good luck? – Joako Dec 03 '21 at 00:34
  • @John as an example, think that your price is the value of a portfolio made by 100 stocks, with some mild assumptions as they are independent, you could end modeling the prices as it is having a Log-Normal distribution (like in Black-Scholes formula). If you made the portfolio as optimal following Markowitz theory at the time $t_0$, since the Log-Normal is an skewed distribution it mean value will be always higher of the mode, so the "real expected value" is lower than the "expected average", meaning here that is much probable to see a real-life realization price series ending in values... – Joako Dec 03 '21 at 16:45
  • @John (...) lower then the mean you have calculated when making the portfolio at time $t_0$, so, your optimal portfolio is still working as planned but because you are seeing a final results lower than the mean value path projection you could think that you need to rearrange your portfolio, when actually it is still being optimal... so thinking that a decision is optimal against the real-path realization is not necessarily "fair"... other issue is if Markowitz theory is right or not (Why not being working with modes instead of means for the optimization problem?), but I can't probe it (yet). – Joako Dec 03 '21 at 16:50
  • 1
    Assume the full history is known and trading happens instantaneously. My simplifying assumption: pick a time step $t$ and assume you observe prices and can only trade at time that are multiples of $t$. Each time step you need to decide what to do with your portfolio. Since there is no uncertainty there are just 3 possible answers: (1) cover your shorts and buy as many shares as you can, (2) sell the shares you own and short as many shares as you can, or (3) do nothing. You should be able to write a Dynamic Program starting at the end, working backwards, incorporating transaction costs. – TickaJules Dec 04 '21 at 21:50

0 Answers0