Say there is a function $f(x)=x^2$
Now take any point $X$ on the line. This will correspond to coordinates $(x,y)$. Now take a small change $dx$ to the left and add it to $x$.
This would mean that the co-ordinates of the new point would move to such that $x_1=x+ dx$ and similarly for $y_1=y + dy$
Difference in these two $y$ or $dy$ equals $$ \begin{aligned} (x+ dx)^2 - x^2 &= x^2-x^2+dx^2+2x\cdot dx \\ &= dx^2+2x\cdot dx \end{aligned} $$
Now as we make $dx$ smaller and smaller $dy$ also gets smaller. We could do this and stop just before the point $X$. Now change in $x$ would be only the point $x_1$ itself I.e. $dx = \text{Point } x_1$.
Since this is a $0$ dimensional quantity, we deduce the following:
$dx^2$ will become 0 as a point multiplied by itself is the point itself(as it is in 2 dimension, I am not saying that the point itself has no value).
Now $dy/dx=2x$ or for every unit time we experience a change of $2x$.
Questions:
Is my use of $dx$ as a point right?
Is my postulate that the distance between two consecutive points is the smallest value there is on a line correct? And if so is it what mathematicians mean by instantaneous rate of change?
Following 2. does this sidestep the paradox of how there exists instantaneous change by describing this change with respect to another point I.e. the point immediately next to it?
So Finally is all a derivative is, is a formula derived from differences between two $y$ values by using the fact that they all have a particular way of increasing (ex. for function of area of circle they increase by its perimeter no matter what $x$ is)?
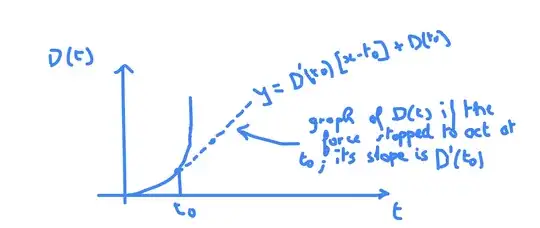
$signs; like this:$x^2\,dx$looks like $x^2,dx$. The\,just adds a small space – FShrike Nov 13 '21 at 11:51