4

Based on the fun of:

Conjectured simple ODE solution: $$y^{(y(x))}(x)=f(x)\mathop \implies\limits^?(y(x))!+c_0Γ(y(x))=\int\limits_{c_1}^xf(t)(x-t)^{y(x)-1} dt $$

Imagine we had a function of which its nth derivative at $x=n$ was some function:

$$\frac{d^{x}y(x)}{dx^x}=y^{(x)}(x)=ax+b\implies y(0)=b\implies y’(1)=a+b,\int y(x)dx\bigg|_{x=-1}=a-b$$

Now let’s use the fractional integral as the inverse of the xth derivative as $x$ is any constant. Therefore we can use Cauchy’s Repeated Integral formula:

$$y^{(x)}(x)=ax+b\implies y(x)+c_1=\text I^{x}_x (ax+b)$$

We can also generalize the lower integration bound as there may be no analog for the indefinite integral:

$$\,_a\text I^n_x g(x)\mathop=^\text{def}\frac 1{Γ(n)}\int_a^xg(t)(x-t)^{n-1}dt \implies y(x)+c_1=\,_{c_0}\text I^x_x (ax+b)= \frac 1{Γ(x)}\int_{c_0}^x(at+b)(x-t)^{x-1}dt \mathop=^{x\ne 0,-1}\\\implies y(x)=^?\frac{(x-c_0)^x(ac_0x+ax+bx+b)}{(x+1)!}+c_1$$

Here is an interactive graph of the conjectured answer.

The problem is that this formula only works for the trivial $a=b=0$ case.

Here is my graphical attempt for $y^{(x)}(x)=1$: $$y(0)=1,y’(1)=1,y’’(1)=1$$

maybe we can assume a function looking like the following with all constants of integration being $0$ for simplicity. Here is the graph with these properties:

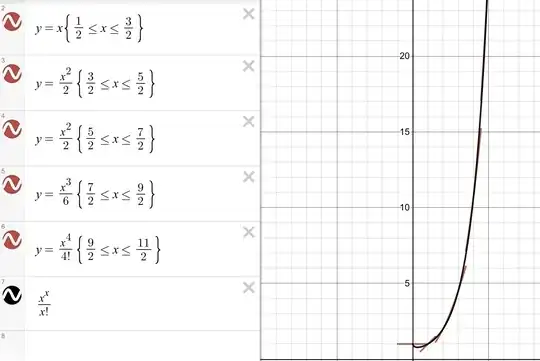enter image description here Notice how this function matches up with our conjectured result:

$$y^{(x)}(x)=1\implies y(x)=\frac{x^x}{x!}$$

Actually we can generalize this process by doing:

$$y^{f(x)}(x)=g(x)\implies y(x)=\text I_x^n g(x),n=f(x)$$

given that $f\ne y$ so that we can solve the equation.

Then just use a definition of the $n$th integral or derivative and to finish.

I have also found this solution $n\in\Bbb N$ derivatives for $ax+b=1$ with many initial conditions:

$$y’’’(x)=1,y(0)=y’(1)=y’’(2)=y’’’(3)=1\implies y^{(n)}(x)=1,y^{(n)}(n)=y^{(n-1)}(n-1)=1=…=y’’(2)=1,y’(1)=1,y(0)=1:$$

which would give the following polynomial for $n=6$:

$$y(x)= \frac1{720} (720 - 4866 x + 4560 x^2 - 1500 x^3 + 270 x^4 - 24 x^5 + x^6), y^{(6)}(6)= y^{(5)}(5)= y^{(4)}(4)= y^{(3)}(3)= y^{(2)}(2) = y’(1)=y(0)=1 $$

Therefore our conjectured solution for $n\in\Bbb N$ is:

$$y=\frac1{n!}\sum_{k=0}^n c_k(-1)^k x^k,$$

where $c_k$ are the coefficients of our solution polynomial which may relate to these Polynomial function.

A self answer found the general solution assuming natural number order derivatives.

Therefore, how can $y^{(x)}(x)=ax+b$ be solved for $y(x)$ using fractional derivatives? Please correct me and give me feedback!

The Art Of Repetition
  • 2,428
  • 1
  • 7
  • 34
Тyma Gaidash
  • 13,576
  • It seems to me that $y(x) = x^x/x!$ does not satisfy $y'(1)=1$ nor $y''(2)=1$ nor $y'''(3) = 1$. – GEdgar Oct 21 '21 at 14:55
  • @GEdgar Note how the question said “ The problem is that this formula only works for the trivial $a=b=0$ case. ” Do you know how we can solve $$y^{(x)}(x)=ax+b$$? Thanks. – Тyma Gaidash Oct 21 '21 at 15:02
  • I tried to find some claim in that lengthy post to test. So, you do not claim that $$y^{(x)}(x)=1\implies y(x)=\frac{x^x}{x!}$$ Is there something that you do claim? – GEdgar Oct 21 '21 at 15:04

1 Answers1

2

Help is needed for solving the differential equation for fractional derivatives.

Maybe if $x\in\Bbb N$, then the following is a finite difference equation. However, the following is a particular solution to $y^{([x])}(x)=ax+b$ with the round $[x]$ or $y^{(x)}(x)=ax+b$ with $n$, $n\in\Bbb N$. Find a pattern for $y^{(x-k)},k\in\Bbb N$

$$y^{(x)}(x)=ax+b,y^{(x-1)}(x)=\frac{ax^2}{1\cdot2}+bx+c_0,y^{(x-2)}(x)=\frac{ax^3}{1\cdot2\cdot3}+\frac{bx^2}{1\cdot2}+c_1x+c_0,\implies y^{(x-k)}=\frac{ax^{k+1}}{(k+1)!}+\frac{bx^k}{k!}+\sum_{n=0}^{k-2}c_nx^n$$

Set $k=[x]$ and rename series coefficients:

$$\boxed{y(x)=a\frac{x^{[x]+1}}{([x]+1)!}+b\frac{x^{[x]}}{[x]!}+\sum_{n=0}^{x-2}c_nx^n}$$

Shown here

Тyma Gaidash
  • 13,576