1

$$\large{\text{Motivation:}}$$

Here is a related Fresnel Integral sum for a seventh in a series of a sum of just a single function:

On $$\mathrm{\sum\limits_{n=0}^\infty \left(C(n)-\frac{\sqrt\pi}{2\sqrt2}\right)+ \sum\limits_{n=0}^\infty \left(S(n)-\frac{\sqrt\pi}{2\sqrt2}\right)}$$

$$\large{\text{Original Problem and Definitions:}}$$

Here I will use the Normalized definition of the Fresnel F and G functions. They are the auxiliary functions which means they are used to prove properties about the Fresnel Integrals functions $\text C(x)$ and $\text S(x)$:

Here are the definitions with the problem:

$$\sum_{\Bbb N^0}( \text G(n)+i\text F(n))\\\mathop=^\text{def} i\sum_{n=0}^\infty \left[\left(\frac12-\int_0^n\sin\left(\frac{\pi n^2}{2}\right)dn\right) \cos\left(\frac{\pi n^2}{2}\right)- \left(\frac12-\int_0^n\cos\left(\frac{\pi n^2}{2}\right)dn\right) \sin\left(\frac{\pi n^2}{2}\right) \right] \\+\sum_{n=0}^\infty \left[\left(\frac12-\int_0^n\cos\left(\frac{\pi n^2}{2}\right)dn\right) \cos\left(\frac{\pi n^2}{2}\right)+ \left(\frac12-\int_0^n\sin\left(\frac{\pi n^2}{2}\right)dn\right) \sin\left(\frac{\pi n^2}{2}\right) \right] \\ = i\sum_{n=0}^\infty\left[\left(\frac12-\text S(n)\right) \cos\left(\frac{\pi n^2}{2}\right) -\left(\frac12-\text S(n)\right) \cos\left(\frac{\pi n^2}{2}\right)\right]\\+ \sum_{n=0}^\infty \left[\left(\frac12-\text C(n)\right) \cos\left(\frac{\pi n^2}{2}\right) +\left(\frac12-\text S(n)\right) \sin\left(\frac{\pi n^2}{2}\right)\right] $$

$$\large{\text{Visualization:}}$$

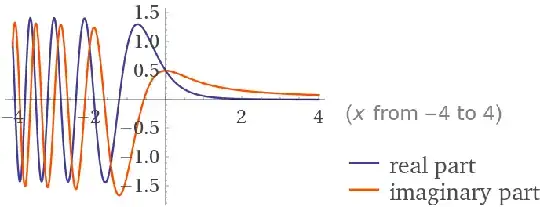
Here is a plot of the summand: enter image description here

I am more interested in the following summations of which the Fresnel F sum diverges and the Fresnel F sum converges. Here are the sums up to thousands of terms:

$$\sum_0^\infty \text G(n)≈0.581217…$$ and $$\sum_0^\infty \text F(n)=\infty$$

$$\large{\text{Useful Identity:}}$$

but there is one nice result using DLMF $7.7.12$ proven true here

$$\sum_{n=0}^\infty \text G(n)+i \text F(n)=\sum_{n=0}^\infty e^{-\frac{i\pi n^2}2}\int_n^\infty e^{\frac{i\pi t^2}2}dt = \sum_{n=0}^\infty e^{-\frac{i\pi n^2}2}\left(\frac12+\frac i2-\text C(n)-i\text S(n)\right)\implies \sum_{n=0}^\infty \text G(n)= \text{Re}\sum_{n=0}^\infty e^{-\frac{i\pi n^2}2}\left(\frac12+\frac i2-\text C(n)-i\text S(n)\right)=\text{Re} \sum_{n=0}^\infty e^{-\frac{i\pi n^2}2}\left(\frac12+\frac i2\bigg)\bigg(1+i\text{erfi}\left((1+i)\frac{\sqrt\pi}2n\right)\right)$$

which can be put in terms of the Floor function or take the real part of the result and use Euler’s Formula

$$\large{\text{Integral Representation:}}$$

or try evaluating:

$$\sum_{n=0}^\infty \text F(n)=\frac1{\pi\sqrt2} \sum_{n=0}^\infty \int_0^\infty \frac{1}{\sqrt t (t^2+1) e^{\frac{\pi n^2 t}2}}dt= \frac1{\pi\sqrt 2} \int_0^\infty \frac{1}{\sqrt t (t^2+1)} \sum_{n=0}^\infty e^{-\frac{\pi n^2 t}2}dt = \frac1{2\sqrt2\pi}\int_0^\infty \frac{\vartheta_3\left(e^{-\frac{\pi t}2}\right)+1}{(t^2+1)\sqrt t}dt=\infty$$

which diverges.

$$\large{\text{Updated Problem:}}$$

So now our goal is: $$\sum_0^\infty \text G(n)$$ Here is an interesting and convergent integral. It has the increasing function of $\sqrt t$ in the numerator strangely making it converge:

$$\sum_{n=0}^\infty \text G(n)\mathop=^\text{def} \sum_{n=0}^\infty \left[\left(\frac12-\text C(n)\right) \cos\left(\frac{\pi n^2}{2}\right) +\left(\frac12-\text S(n)\right) \sin\left(\frac{\pi n^2}{2}\right)\right]=\frac1{\pi\sqrt2} \sum_{n=0}^\infty \int_0^\infty \frac{\sqrt t}{ (t^2+1)e^{\frac{\pi n^2 t}2}} dt= \frac1{\pi\sqrt 2} \int_0^\infty \frac{\sqrt t}{ (t^2+1)}\sum_{n=0}^\infty e^{-\frac{\pi n^2 t}2}dt = \frac1{2\sqrt2\pi}\int_0^\infty \frac{\sqrt t\left[\vartheta_3\left(e^{-\frac{\pi t}2}\right)+1\right]}{t^2+1}dt = \frac1{2\sqrt2\pi}\int_0^\infty \frac{\sqrt t\,\vartheta_3\left(e^{-\frac{\pi t}2}\right)}{t^2+1}dt+ \frac1{2\sqrt2\pi}\int_0^\infty \frac{\sqrt t}{t^2+1}dt = \frac1{2\sqrt2\pi}\int_0^\infty \frac{\vartheta_3\left(e^{-\frac{\pi t}2}\right)\sqrt t}{t^2+1}dt +\frac14$$

of which the partial sum has a closed form in terms of the special case Jacobi Theta functions of the Third Kind $\vartheta_3(0,x)=\vartheta_3(x)$ which can be put in terms of simpler elliptic functions.

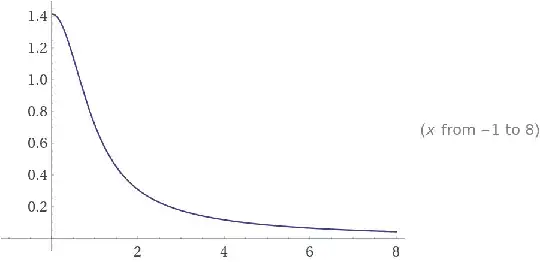
$$\large{\text{Integrand Visualization:}}$$

Here is a plot of $\frac{\vartheta_3\left(e^{-\frac{\pi t}2}\right)\sqrt t}{t^2+1}$:

enter image description here According to Wolfram Functions $9.3.3.6.1$, we can simplify to:

$$\boxed{\sum_0^\infty \text G(n)= \sum_{n=0}^\infty \left[\left(\frac12-\text C(n)\right) \cos\left(\frac{\pi n^2}{2}\right) +\left(\frac12-\text S(n)\right) \sin\left(\frac{\pi n^2}{2}\right)\right]= \frac1{2\sqrt2\pi}\int_0^\infty \frac{\vartheta_3\left(e^{-\frac{\pi t}2}\right)\sqrt t}{t^2+1}dt +\frac14 = \frac{\sqrt i}{2\sqrt2\pi}\int_0^\infty \frac{\vartheta_3\left(e^{-\frac{2i}t}\right)}{t^2+1}dt +\frac14 }$$

$$\large{\text{Conclusion}}$$

How can I evaluate the Normalized Fresnel G sum? If there is a closed form, then please write it, but it is optional. Please correct me and give me feedback!

Тyma Gaidash
  • 13,576
  • 3
    If I understand correctly, you can write $\sum_{n=0}^\infty$ and use $n$ in the upper limits of integration, right? As it stands, you've left the index of summation ambiguous and overloaded the letter $x$, which is pointlessly rebellious and reading it is like scrubbing my brain with sandpaper. – anon Oct 12 '21 at 03:58
  • @runway44 If only used one variable,$x$ in this case, then you can assume that $$\sum_a^b \text{sequence}n=\sum{n=a}^b \text{sequence}n,\int_a^b f(x) dx=\int{x=a}^{x=b} f(x)dx$$ because there is no ambiguity on the variable of the sum nor integral, which uses a differential telling with respect to which variable. It is easier to type and $x$ is still a variable that can be used, like most other operations. How could I evaluate the sum? – Тyma Gaidash Oct 12 '21 at 11:43
  • 1
    Please use $n$ ($k$ etc.) for a discrete (integer) summation variable, refer to it in the summation subscript, and reserve $x$ ($t$ etc.) for a continuous (real) variable, like everyone else. Your present notation is needlessly hard to read. – John Bentin Oct 12 '21 at 20:59
  • @JohnBentin Let me change the variable, but note that I used $x$ in other posts. – Тyma Gaidash Oct 12 '21 at 21:36
  • @JohnBentin The post is now “fixed”. Did I miss any “x”s? – Тyma Gaidash Oct 12 '21 at 22:04
  • 1
    You've overloaded "n" in the integrals in the formulas preceding the first figure. You're using $n$ as both the integration variable and as the integration limit. Also it's a bit confusing that you reference DLMF which is primarily about the non-normalized versions, but the question seems to be about the normalized versions. Are you sure all of the formulas you quote from DLMF apply to the normalized versions? – Steven Clark Oct 13 '21 at 04:11
  • I am giving up on this one! – John Bentin Oct 13 '21 at 05:09
  • @StevenClark Yes they are all for the Normalized versions. I checked both numerically here with the real part≈ .518 and here with the Integral having the exact same value. I had to use n in the integral for the definition, for example Normalized S(x), $$\text S(n)=\int_0^n \sin\bigg(\frac{\pi x^2}2\bigg)dx$$ – Тyma Gaidash Oct 13 '21 at 11:50
  • 1
    This is how you should have written the integrals in the formulas preceding the first figure. You went too far in converting $x$'s to $n$'s. The integration variable should be the continuous variable $x$, and the integration limit should be the integer value $n$. The first integral sum which corresponds to $i,F(n)$ also seems to be missing a preceding $i$. – Steven Clark Oct 13 '21 at 16:13
  • Your partial evaluation $\sum\limits_{n=0}^{1000} G(n)\approx 0.581217$ seems correct, but $\sum\limits_{n=0}^{1000} F(n)\approx 2.84118$ (I'm not sure how you came up with $3.41028$). Mathematica gives the following numerical evaluations: $\sum\limits_{n=0}^\infty G(n)\approx 0.5812169998766582$ and $\sum\limits_{n=0}^\infty F(n)\approx 7453.103433802164$, but generates a couple of error messages for the second evaluation. – Steven Clark Oct 13 '21 at 16:16
  • @StevenClark The FresnelF sum almost certainly diverges. I just included it because I did not know it’s convergence until I found out when working on the question. Even with a few typos, the main idea of the question still stands. Thanks again. – Тyma Gaidash Oct 13 '21 at 17:12
  • @StevenClark You can also try to solve the equivalent $$\sum_{\Bbb N^0}\text G(n)= \frac1{2\sqrt2\pi}\int \limits_0^\infty \frac{\vartheta_3\left(e^{-\frac{\pi x}2}\right)\sqrt x}{x^2+1}dx +\frac14 $$ which uses a Jacobi Theta function converging to $.5812…$. Thanks. – Тyma Gaidash Oct 13 '21 at 17:30
  • 1
    I thought the main idea was to evaluate $\sum\limits_{n=0}^\infty G(n)+i,F(n)$. It's too bad if $\sum\limits_{n=0}^\infty F(n)$ diverges because as you said $G(z)+i,F(z)=e^{-\frac{1}{2} \pi i z^2} \int_z^{\infty } e^{\frac{1}{2} \pi i t^2},dt$ is a nice result. – Steven Clark Oct 13 '21 at 18:05
  • @StevenClark Correct, but in the very end, that “nice result” would be a number with infinite magnitude: $.5812+…+ i\infty$, like here. You can also evaluate the “nice result” if you want, but please separate the real and imaginary parts at the end. Thanks! Also see DLMF 7.7.12. What do you think? – Тyma Gaidash Oct 13 '21 at 18:22
  • Let us continue this discussion in chat. – Тyma Gaidash Oct 13 '21 at 18:27

0 Answers0