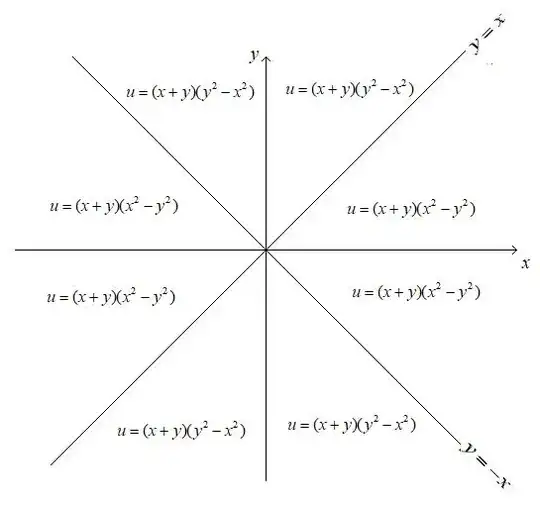
$\begin{cases} yu_x+xu_y=u\\u(x,0) = x^3 \\ u(0,y)=y^3\end{cases}$
$\dot X(\sigma,s)=Y \quad X(\sigma,0)=\sigma \\ \dot Y(\sigma,s)=X \quad Y(0,s)=s \\ \dot U(\sigma,s)=U \quad U(\sigma,0)=\sigma^3\quad and \quad U(0,s)=s^3$
$\frac{dU}{ds}=U\implies U(\sigma,s) = Ce^s$ (1)
$\frac{dX}{ds}=Y\implies$ $\frac{d^2X}{ds^2}=\frac{dY}{ds}=X\implies \ddot X=X\implies$
$X(\sigma,s)=C_1 e^s+C_2 e^{-s}$ (2) and since $\dot X=Y\implies$
$Y(\sigma,s)=C_1 e^s-C_2 e^{-s}$ (3)
applying $X(\sigma,0)=\sigma$ has no issues to find $C_1+C_2=\sigma$, but what with $Y(0,s)=s$ or did I assume wrong initial conditions?