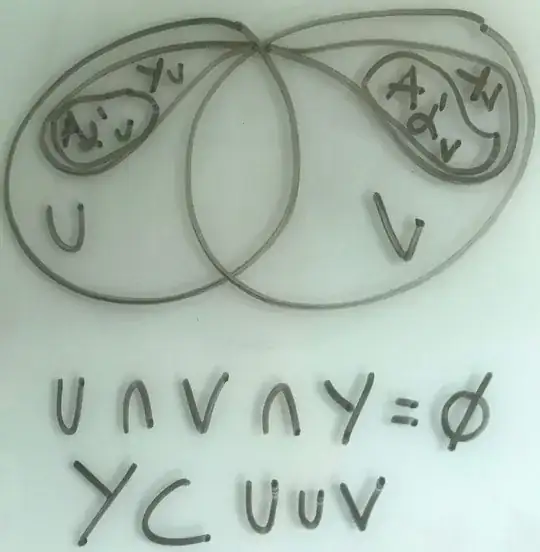Let $\mathscr{F}$ be a collection of connected subsets of a metric space $M$ such that $\bigcap\mathscr{F}\ne\emptyset$. Prove that $\bigcup\mathscr{F}$ is connected.
If $\bigcup\mathscr{F}$ is not connected, then it can be partitioned into two disjoint, non-empty subsets $A,B$. Let $x$ be a point in $\bigcap\mathscr{F}$. Then either $x\in A$ or $x\in B$. I don't know where to go from here.
HINT: You’re actually about halfway there, though you omitted an important qualification of $A$ and $B$: if $\bigcup\mathscr{F}$ is not connected, then it can be partitioned into two disjoint, non-empty, relatively open subsets $A$ and $B$. Now fix $x\in\bigcap\mathscr{F}$, and without loss of generality assume that $x\in A$. $B\ne\varnothing$, so pick any $y\in B$. Then there is some $F\in\mathscr{F}$ such that $y\in F$, and of course $x\in F$. Thus, $x\in A\cap F$, and $y\in B\cap F$, so $A\cap F\ne\varnothing\ne B\cap F$. Why is this a contradiction?
Use that $X$ is connected if and only if the only continuous functions $f:X\to\{0,1\}$ are constant, where $\{0,1\}$ is endowed with the discrete topology.
Now, you know each $F$ in $\mathscr F$ is connected. Consider $f:\bigcup \mathscr F\to\{0,1\}$, $f$ continuous.
Take $\alpha \in\bigcap\mathscr F$. Look at $f(\alpha)$, and at $f\mid_{F}:\bigcup \mathscr F\to\{0,1\}$ for any $F\in\mathscr F$.
Since you mention metric spaces, I am not sure if you know about the first thing I mention, so let's prove it:
THM Let $(X,\mathscr T)$ be a metric (or more generally, a topological) space. Then $X$ is connected if and only if whenever $f:X\to\{0,1\}$ is continuous, it is constant. The space $\{0,1\}$ is endowed with the discrete metric (topology), that is, the open sets are $\varnothing,\{0\},\{1\},\{0,1\}$.
P First, suppose $X$ is disconnected, say by $A,B$, so $A\cup B=X$ and $A\cap B=\varnothing$, $A,B$ open. Define $f:X\to\{0,1\}$ by $$f(x)=\begin{cases}1& \; ; x\in A\\0&\; ; x\in B\end{cases}$$
Then $f$ is continuous because $f^{-1}(G)$ is open for any open $G$ in $\{0,1\}$ (this is simply a case by case verification), yet it is not constant. Now suppose $f:X\to\{0,1\}$ is continuous but not constant. Set $A=\{x:f(x)=1\}=f^{-1}(\{1\})$ and $B=\{x:f(x)=0\}=f^{-1}(\{0\})$. By hypothesis, $A,B\neq \varnothing$. Morover, both are open, since they are the preimage of open sets under a continuous map, and $A\cup B=X$ and $A\cap B=\varnothing$. Thus $X$ is disconnected. $\blacktriangle$
I like "clopen" sets... it is a set that is at the same time closed and open. A topological space $X$ is not connected if, and only if, for any point $a \in X$, you have a "non-trivial" clopen set $C$ containing $a$. That is, a clopen set such that $\emptyset \neq C \subsetneq X$.
Take $a \in \bigcap \mathscr{F}$. Then, take a clopen set $C \subset \bigcup \mathscr{F}$ containing $a$. In the relative topology, for any $X \in \mathscr{F}$, $C \cap X$ is a clopen set. Since $X$ is connected, $C \cap X = X$. That is, $X \subset C$ for every $X \in \mathscr{F}$. Therefore, $\bigcup \mathscr{F} \subset C$.
Therefore, $\bigcup \mathscr{F}$ has no "non-trivial" clopen set, and so, it is connected.
The proof admits some variants. For example, if you take any non-empty clopen set $C'$, it will intersect some $X \in \mathscr{F}$. From connectedness, we have that $X \subset C'$. In particular, $a \in C'$.
The quickest way is using functions from $\bigcup\mathcal{F}$ to $\{0,1\}$, However you can do it directly.
Let $A, B$ be a partition of $\bigcup\mathcal{F}$ into open, disjoint subsets. WLOG assume that $A$ is non-empty. Then there is some $x\in A$ and hence some $F\in \mathcal{F}$ so that $x\in F$. As $F$ is connected it follows that $F\subseteq A$, hence $\bigcap \mathcal{F} \subseteq F \subseteq A$. As this intersection is non-empty every $G\in \mathcal{F}$ has a point in $A$ and by the connectness of each $G$ then $G\subseteq A$. Hence every member of $\mathcal{F}$ is a subset of $A$ and so $B$ is empty.
Here is a proof which never needs to refer to any point in the space itself.
Assume for the sake of contradiction that $A\cup B=\bigcup \mathcal{F}$ where $A,B$ are open (in $\bigcup\mathcal{F}$) and non-trivial, and disjoint.
If we then suppose that each $F\in \mathcal{F}$ is contained in $A$, we get $B=\emptyset$, a contradiction. So there is at least one $F_A$ which is not contained in $A$. Suppose $F_A$ is not entirely contained in $B$, then it is disconnected with seperation $$(F_A\cap A)\cup (F_A\cap B) $$ where each component of the partition is open relative to $F_A$. This is a contradiction.
So $F_A$ is entirely contained in $B$. Similarly, we can find $F_B$ entirely contained in $A$, and then $$F_A\cap F_B=\emptyset.$$ A contradiction.
Denote the whole topology space as $(\bigcup \mathcal{F},\mathcal{T})$.
Suppose $\bigcup \mathcal{F}$ is not connected, then there exists disjoint two non-empty open sets $A,B$ that decompose $\bigcup \mathcal{F}$, that is , $A,B \neq \emptyset$, $A \bigcap B = \emptyset$, $A \bigcup B = \bigcup \mathcal{F}$ and $A,B\in\mathcal{T} $.
Since $\bigcap \mathcal{F} \neq \emptyset$, so $\exists x \in \bigcap \mathcal{F}$, W.L.O.G we assume $x \in A$.
Meanwhile, since $B \neq \emptyset$, we know $B \bigcap \mathcal{F}_j \neq \emptyset$ for some $\mathcal{F}_j$, and $\exists y \in B \bigcap \mathcal{F}_j$.
Then we claim that $\mathcal{F}_j$ can be decomposed into two non-empty disjoint open sets $A \bigcap \mathcal{F}_j$ and $B \bigcap \mathcal{F}_j$. This is because, $x \in A \bigcap \mathcal{F}_j \Rightarrow (A \bigcap \mathcal{F}_j) \neq \emptyset$; $y \in B \bigcap \mathcal{F}_j \Rightarrow (B \bigcap \mathcal{F}_j) \neq \emptyset$;
$A \bigcap B = \emptyset \Rightarrow (A \bigcap \mathcal{F}_j) \bigcap (B \bigcap \mathcal{F}_j) = \emptyset$;
$A \bigcup B = \bigcup \mathcal{F} \Rightarrow (A \bigcap \mathcal{F}_j) \bigcup (B \bigcap \mathcal{F}_j) = (A \bigcup B) \bigcap \mathcal{F}_j = \mathcal{F}_j$;
$A,B \in \mathcal{T} \Rightarrow (A \bigcap \mathcal{F}_j), (B \bigcap \mathcal{F}_j) \in \mathcal{T}_{F_j}$, where $(\mathcal{F}_j,\mathcal{T}_{F_j})$ is the induced subspace.
The above claim contradicts with the assumption that each $\mathcal{F}$ is connected, hence we know $\bigcup \mathcal{F}$ is connected.
We begin with a Lemma:
If $X$ is a topological space with separation $A \cup B$ and $Y \subset X$ is connected, then $Y \subset A$ or $Y \subset B$. The proof goes by noticing that $(Y \cap A) \cup (Y \cap B)$ is a disconnection of $Y$. Which cannot happen as $Y$ is connected.
Now for main proof: Let us suppose $\bigcup \mathcal{F} = A \cup B$ where $A,B$ are disjoint open nonempty subsets of our space $M$. Then there exists some $x \in \bigcap \mathcal{F}$. WLOG say $x \in A$. But $B$ is nonempty thus there exists some $b \in B$ forcing $b \in \mathcal{F}_\beta$ for some $\beta$ in our indexing set. But as $x \in \bigcap \mathcal{F}$ we have $x \in \mathcal{F}_\beta$ but by our lemma $\mathcal{F}_\beta \subset A$ or $\mathcal{F}_\beta \subset B$ thus the union is connected.
Proof: Suppose the contrary. Let $A$ and $B$ be nonempty open subsets partition of $\cup\scr F$. There are subsets $F_1, F_2\in \mathscr F\ni (F_1\cap A \neq\emptyset \wedge F_2\cap B\neq\emptyset)$. $A\cup B \supseteq F_1\cup F_2$, it cannot be true $F_1\subseteq A\wedge F_2 \subseteq B$ since $F_1\cap F_2\neq \emptyset$. Without loss of generality, we suppose $F_1\cap B\neq\emptyset$. Then $F_1\cap A$ and $F_1\cap B$ are nonempty open partition of $F_1$ contradicting the connectedness of $F_1$.$\quad \square$
Key Lemma: Let $F$ be a connected set and $U,V$ be disjoint open sets such that $F\subset U\cup V$. Then either $F\subset U$ or $F\subset V.$
Now, let $\cal F$ be a collection of connected sets such that $x\in\cap_{F\in\cal F} F\neq\emptyset$.
Assume that $X=\cup_{F\in\cal F}F$ is disconnected so that there are disjoint open sets $U,V$ such that $X\subset U\cup V$, $X\cap U\neq\emptyset$ and $X\cap V\neq\emptyset$. WLOG $x\in U$. But then due to key lemma each $F\in\cal F$ is a subset of $U$ contradicting the fact that $X$ intersects $V$.
Let $X$ be a space and $\{A_\alpha:\alpha \in I\}$ a family of connected subsets of $X$ for which $\bigcap\limits_{\alpha \in I} A_\alpha \ne \emptyset$.
Let first modify the notation a little bit. We modify $\bigcup \mathscr{F}$ in the question into $Y = \bigcup\limits_{\alpha \in I} A_\alpha$.
We will use this Theorem 1 to prove that $Y$ is connected: (For the curious minds, the proof of Theorem 1 itself is outlined below.)
$Y$ is disconnected if and only if there exist open sets $U$ and $V$ in $X$ such that:
$U \cap Y \ne \emptyset$; $V \cap Y \ne \emptyset$; $U \cap V \cap Y = \emptyset$; $Y \subset U \cup V$.
Note that $U$ and $V$ are not necessarily disjoint.
Suppose that $U$ and $V$ are open sets in $X$ for which $U \cap Y \ne \emptyset$; $U \cap V \cap Y = \emptyset$; $Y \subset U \cup V$. We will show that $V \cap Y = \emptyset$ thus proving that $Y$ is connected.
As $U \cap Y \ne \emptyset$, so $U$ contains some points in $A_{\alpha'}$ for some $\alpha' \in I$. We know that $Y \subset U \cup V$ which means $A_{\alpha'}$ could be in both $U$ and $V$ as well. However, because $(U \cap A_{\alpha'}) \cap (V \cap A_{\alpha'}) = U \cap V \cap A_{\alpha'} \subseteq U \cap V\cap Y = \emptyset$, we know that if $A_{\alpha'}$ are in both $U$ and $V$, then it would be disconnected. As $A_{\alpha'}$ is connected by definition, $A_{\alpha'}$ must be either in $U$ or $V$, so $A_{\alpha'} \subset U$.
Refer to this picture for a clearer visualization of when both $A_{\alpha'}$ are present in both $U$ and $V$. This situation leads to the disconnection into $A_{{\alpha'}_U}$ and $A_{{\alpha'}_V}$:
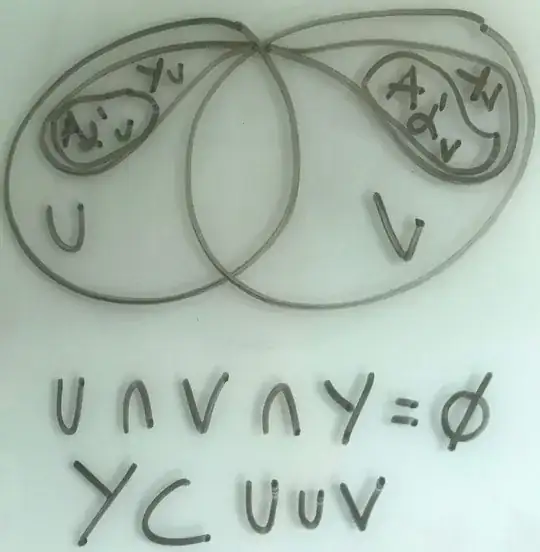
If $b \in \bigcap\limits_{\alpha \in I} A_\alpha$, then $b$ must be in $A_{\alpha'}$, so $b \in U$. Thus U contains a point b in each $A_\alpha$, $\alpha \in I$. By the same reasoning above and as $A_\alpha$ is connected, then $A_\alpha \in U$ for each $\alpha \in I$.
Thus:
$Y = \bigcup\limits_{\alpha \in I} A_\alpha \subset U$.
Which leaves nothing remaining for $V$, so:
$V \cap Y = \emptyset$.
Proof of Theorem 1:
Suppose that Y is disconnected. Then there are non-empty open sets $A$ and $B$ in the subspace topology for $Y$ such that $Y = A \cup B$ and $A \cap B = \emptyset$. By the definition of relatively open sets, there must be open sets $U$ and $V$ in $X$ such that:
$A = U \cap Y$, $B = V \cap Y$.
So:
$U \cap V \cap Y = (U \cap Y) \cap (V \cap Y) = A \cap B = \emptyset$; $Y = A \cup B = (U \cap Y) \cup (V \cap Y) \subset U \cup V$.
For the reverse implication:
$A \cap B = (U \cap Y) \cap (V \cap Y) = U \cap V \cap Y = \emptyset$; $A \cup B = (U \cap Y) \cup (V \cap Y) = (U \cup V) \cap Y$, and since $Y \subset U \cup V$, $A \cup B = Y$.
There is a generalised version. If $\{F_\alpha:\alpha\in\Lambda\}$ be arbitrary subsets of a metric space with non-empty pairwise intersection. Then also $F=\cup_\alpha F_\alpha$ is connected.
Consider, $f:F\to \{0,1\}$, a continuous map. Take, $x$ from $f^{-1}(1)$ and $y$ from $f^{-1}(0)$. Then, $x\in F_\alpha$ and $y\in F_\beta$ for some $\alpha,\beta\in\Lambda$. Observe, $f(F_\alpha)=\{1\}$ and $f(F_\beta)=\{0\}$. But, for some $z\in F_\alpha\cap F_\beta$, $f(z)$ has no well defined value. $F_\beta$ say it should be $0$ whereas $F_\alpha$ say’s it’s $1$. A contradiction.
So, any continuous map must be constant. Hence, $X$ is connected.
