This is a problem that a friend of mine gave to me a while back. I somewhat solved it and paid no attention to it afterwards until I though about it now. Forgive the errors and laziness this was a long time ago and not everything has to be perfect.
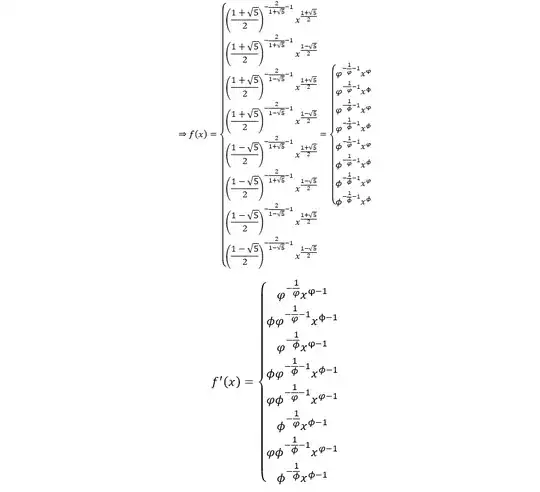
I assumed $f$ to be a polynomial function of the kind $f(x)=ax^b$ where $f^{-1}(x)= \big(\frac x a\big)^{1/b} $ and found $$f(x)= \varphi^{-\frac{1}{\varphi}-1}(-x)^{\phi} $$
where $\varphi=\frac{1+\sqrt{5}}{2}$ and $\phi=\frac{1-\sqrt{5}}{2}$ my working is in the following images : (I did this in word)
I was curious if there were more solutions to just this polynomial? Perhaps a different function ?
Don't bother commenting trying to correct my work I am just curious about the above questions. Thank you for your time